làm ý c thôi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
làm ý b và c thôi nhé
VD
16 tháng 3 2022
b, Thay x=1 vào g(x) ta có:
\(g\left(1\right)=100.1^{100}+99.1^{99}+...+2.1^2+1+1\\ =100.1+99.1+...+2.1+1+1\\ =100+99+...+2+1+1\\ =\left(100+1\right).100:2+1\\ =5051\)
c, Thay x=-1 vào h(x) ta có:
\(h\left(-1\right)=1-\left(-1\right)+\left(-1\right)^2-\left(-1\right)^3+...+\left(-1\right)^{100}\\ =1+1+1+...+1\\ =101\)
30 tháng 12 2023
2: Tọa độ A là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m-2\right)x+m-1=0\left(m-2\right)+m-1=m-1\end{matrix}\right.\)
=>A(0;m-1)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\\left(m-2\right)x+m-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x\left(m-2\right)=-\left(m-1\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{-\left(m-1\right)}{m-2}\\y=0\end{matrix}\right.\)
Vậy: \(B\left(\dfrac{-m+1}{m-2};0\right)\)
\(OA=\sqrt{\left(0-0\right)^2+\left(m-1-0\right)^2}=\sqrt{0+\left(m-1\right)^2}=\sqrt{\left(m-1\right)^2}=\left|m-1\right|\)
\(OB=\sqrt{\left(\dfrac{-m+1}{m-2}-0\right)^2+\left(0-0\right)^2}\)
\(=\sqrt{\left(-\dfrac{m-1}{m-2}\right)^2+0}=\left|\dfrac{m-1}{m-2}\right|\)
Vì Ox\(\perp\)Oy
nên OA\(\perp\)OB
=>\(S_{OAB}=\dfrac{1}{2}\cdot\left|m-1\right|\cdot\dfrac{\left|m-1\right|}{\left|m-2\right|}=\dfrac{1}{2}\cdot\dfrac{\left(m-1\right)^2}{\left|m-2\right|}\)
Để \(S_{OAB}=1\) thì \(\dfrac{1}{2}\cdot\dfrac{\left(m-1\right)^2}{\left|m-2\right|}=1\)
=>\(\left(m-1\right)^2=2\left|m-2\right|\)(1)
TH1: m>=2
Phương trình (1) sẽ trở thành: \(\left(m-1\right)^2=2\left(m-2\right)\)
=>\(m^2-2m+1-2m+4=0\)
=>\(m^2-4m+5=0\)
=>\(\left(m-2\right)^2+1=0\)(vô lý)
TH2: m<2
Phương trình (1) sẽ trở thành:
\(\left(m-1\right)^2=2\left(-m+2\right)\)
=>\(m^2-2m+1=-2m+4\)
=>m2=3
=>\(\left[{}\begin{matrix}m=\sqrt{3}\left(nhận\right)\\m=-\sqrt{3}\left(nhận\right)\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 8 2021
a. \(f\left(x\right)_{max}=f\left(-2\right)=111\) ; \(f\left(x\right)_{min}=f\left(1\right)=-6\)
b. \(f\left(x\right)_{max}=f\left(-3\right)=7\) ; \(f\left(x\right)_{min}=f\left(0\right)=1\)
c. \(f\left(x\right)_{max}=f\left(4\right)=\dfrac{2}{3}\) ; \(f\left(x\right)_{min}\) ko tồn tại
d.
Miền xác định: \(D=\left[-2\sqrt{2};2\sqrt{2}\right]\)
\(y'=\dfrac{2\left(4-x^2\right)}{\sqrt{8-x^2}}=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)
\(f\left(-2\sqrt{2}\right)=f\left(2\sqrt{2}\right)=0\)
\(f\left(-2\right)=-4\) ; \(f\left(2\right)=4\)
\(f\left(x\right)_{max}=f\left(2\right)=4\) ; \(f\left(x\right)_{min}=f\left(-2\right)=-4\)
22 tháng 10 2021
Bài 1:
a: \(A=2\sqrt{3}-\sqrt{27}+\sqrt{4-2\sqrt{3}}\)
\(=2\sqrt{3}-3\sqrt{3}+\sqrt{3}-1\)
=-1
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 1 2022
\(\Rightarrow\left\{{}\begin{matrix}x+my=m+1\\m^2x+my=2m^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+my=m+1\\\left(m^2-1\right)x=2m^2-m-1\end{matrix}\right.\)
Phương trình có nghiệm duy nhất khi \(m^2-1\ne0\Rightarrow m\ne\pm1\)
Khi đó ta có: \(x=\dfrac{2m^2-m-1}{m^2-1}=\dfrac{\left(m-1\right)\left(2m+1\right)}{\left(m-1\right)\left(m+1\right)}=\dfrac{2m+1}{m+1}\)
\(\Rightarrow y=2m-mx=\dfrac{m}{m+1}\)
Để \(\left\{{}\begin{matrix}x\ge2\\y\ge1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{2m+1}{m+1}\ge2\\\dfrac{m}{m+1}\ge1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{-1}{m+1}\ge0\\\dfrac{-1}{m+1}\ge0\end{matrix}\right.\)
\(\Rightarrow m+1< 0\Rightarrow m< -1\)
12 tháng 9 2023
b: \(=\dfrac{9}{2}\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{98\cdot100}\right)\)
\(=\dfrac{9}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{98}-\dfrac{1}{100}\right)\)
\(=\dfrac{9}{2}\cdot\dfrac{49}{100}=\dfrac{441}{200}\)
Y
1 tháng 8 2023
\(1,x=9\Rightarrow A=\dfrac{2\sqrt{9}+1}{\sqrt{9}}=\dfrac{2.3+1}{3}=\dfrac{7}{3}\)
\(2,B=\dfrac{x-3\sqrt{x}+4}{x-2\sqrt{x}}-\dfrac{1}{\sqrt{x}-2}\left(dk:x>0,x\ne4\right)\\ =\dfrac{x-3\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}-\dfrac{1}{\sqrt{x}-2}\\ =\dfrac{x-3\sqrt{x}+4-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{x-4\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
\(3,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-2}{\sqrt{x}}:\dfrac{2\sqrt{x}+1}{\sqrt{x}}=\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}\)
Ta có : \(\left|P\right|+P=0\Leftrightarrow\left|P\right|=-P\)
\(TH_1:x\ge4\\ \dfrac{\sqrt{x}-2}{2\sqrt{x}+1}=-\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}\Leftrightarrow\dfrac{2\left(\sqrt{x}-2\right)}{2\sqrt{x}+1}=0\Leftrightarrow2\sqrt{x}=4\Leftrightarrow x=4\left(tm\right)\)
\(TH_2:x< 4\\ -\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}=-\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}\left(LD\right)\)
Vậy \(x=4\) thì thỏa mãn đề bài.
QN
0
2 tháng 3 2022
1: \(A=-\dfrac{1}{3}\cdot3\cdot x\cdot x^3\cdot y\cdot z^2=-x^4yz^2\)
2: \(A=-1^4\cdot\left(-1\right)\cdot2^2=4\)
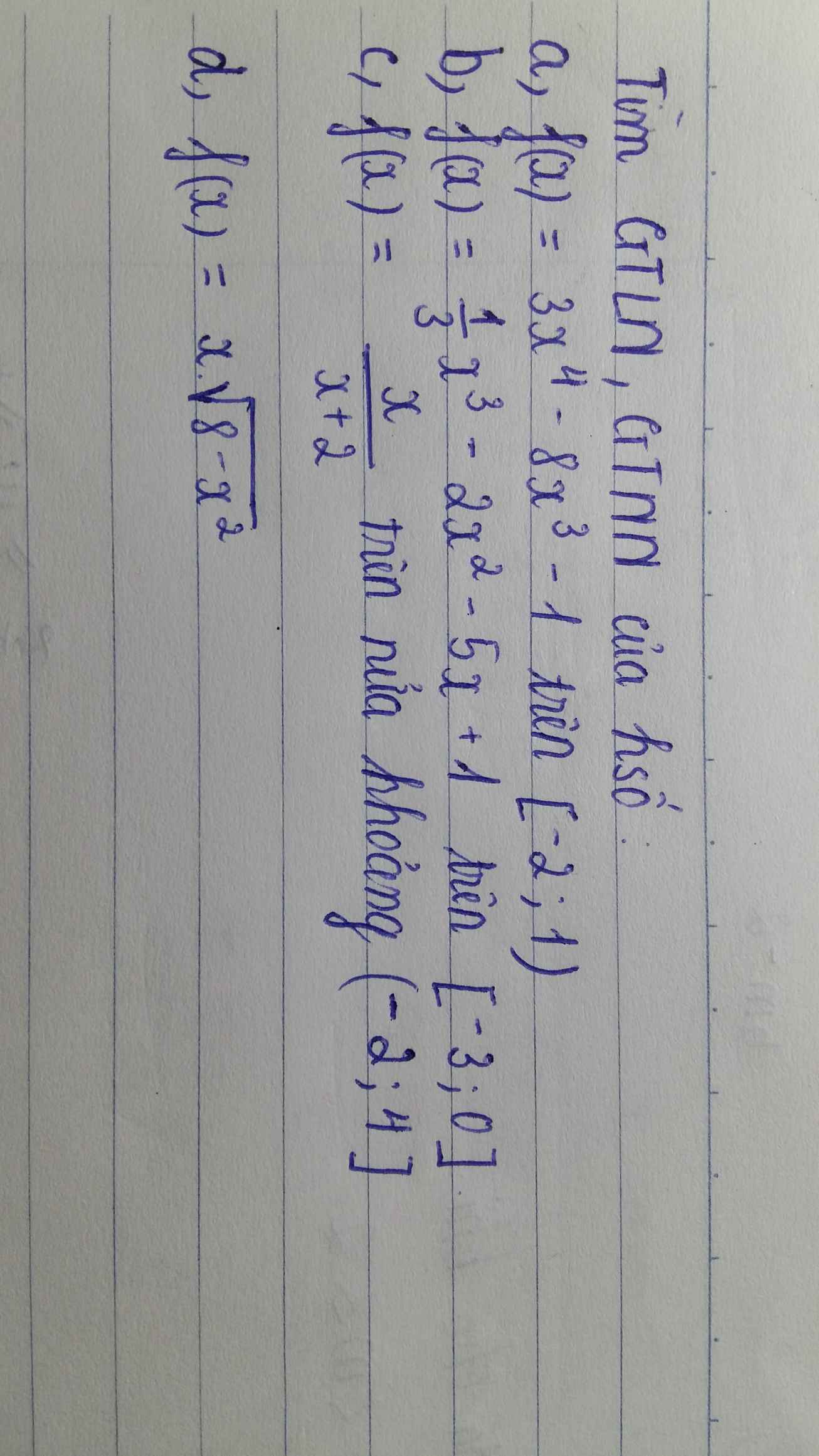
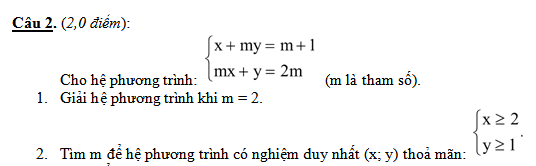
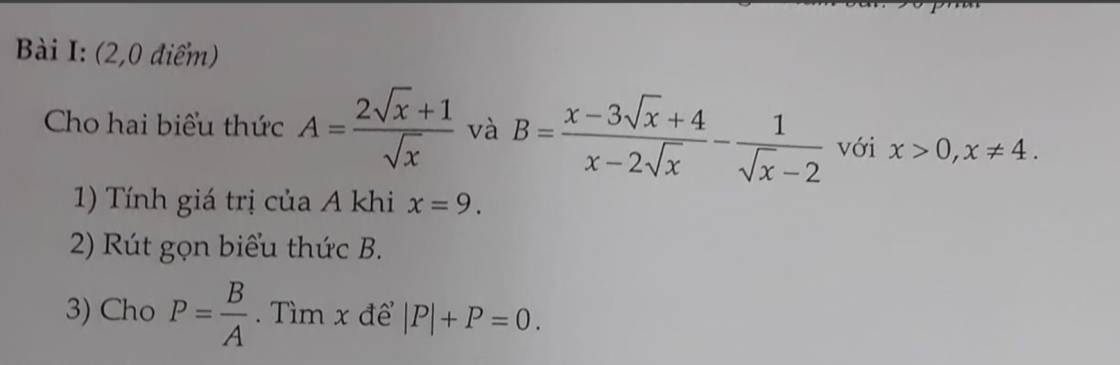
b: Thay x=-1 vào (P), ta được:
y=(-1)^2=1
=>A(-1;1)
Thay x=2 vào (P), ta được:
y=2^2=4
=>B(2;4)
Gọi (AB): y=ax+b
Vì AB đi qua A,B nên ta có hệ:
-a+b=1 và 2a+b=4
=>a=1; b=2
=>y=x+2
c: (d): y=ax+b
Vì (d)//AB nên (d): y=x+b
PTHĐGĐ là:
x^2-x-b=0
Δ=(-1)^2-4*1*(-b)=4b+1
Để (d) tiếp xúc với (P) thì 4b+1=0
=>b=-1/4
=>(d): y=x-1/4