Trên mặt phẳng tọa độ Oxy, cho tam giác ABC với tọa độ các đỉnh là A(1; 2), B(3; 4), C(6; 1). Phương trình đường thẳng chứa đường cao AH của tam giác đó có hệ số góc là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MK
20 tháng 12 2021
1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2021
Bạn coi lại đề, 2 đường thẳng xuất phát từ B nhưng lại song song với nhau, điều này hoàn toàn vô lý
26 tháng 3 2023
Gọi B',C' lần lượt là chân đường phân giác kẻ từ B,C xuống lần lượt AC,AB
GỌi i là giao của BB' và CC'
Tọa độ I là:
x-1=0 và x-y-1=0
=>x=1 và y=0
Kẻ IH vuông góc AC tại H
=>H(2;-3)
=>vecto AH=(-2;-2)=(1;1)
Phương trình AH là:
1(x-4)+1(y+1)=0
=>x+y-3=0
=>AC: x+y-3=0
Tọa độ C là:
x+y-3=0 và x-y-1=0
=>C(2;1)
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
Ta có: \(\overrightarrow {AB} = \left( {4;1} \right),\overrightarrow {AC} = \left( {3;3} \right),\overrightarrow {BC} = \left( { - 1;2} \right)\)
+) Đường thẳng AB nhận vectơ \(\overrightarrow {AB} = \left( {4;1} \right)\)làm phương trình chỉ phương nên có vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {1; - 4} \right)\) và đi qua điểm \(A(1;1)\), suy ra ta có phương trình tổng quát của đường thẳng AB là:
\(\left( {x - 1} \right) - 4\left( {y - 1} \right) = 0 \Leftrightarrow x - 4y + 3 = 0\)
Độ dài đường cao kẻ từ C chính là khoảng cách từ điểm C đến đường thẳng AB
\(d\left( {C,AB} \right) = \frac{{\left| {4 - 4.4 + 3} \right|}}{{\sqrt {{1^2} + {4^2}} }} = \frac{{9\sqrt {17} }}{{17}}\)
+) Đường thẳng BC nhận vectơ \(\overrightarrow {BC} = \left( { - 1;2} \right)\)làm phương trình chỉ phương nên có vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {2;1} \right)\) và đi qua điểm \(B(5;2)\), suy ra ta có phương trình tổng quát của đường thẳng BC là:
\(2\left( {x - 5} \right) + \left( {y - 2} \right) = 0 \Leftrightarrow 2x + y - 12 = 0\)
Độ dài đường cao kẻ từ A chính là khoảng cách từ điểm A đến đường thẳng BC
\(d\left( {A,BC} \right) = \frac{{\left| {2.1 + 1 - 12} \right|}}{{\sqrt {{2^2} + {1^2}} }} = \frac{{9\sqrt 5 }}{5}\)
+) Đường thẳng AC nhận vectơ \(\overrightarrow {AC} = \left( {3;3} \right)\)làm phương trình chỉ phương nên có vectơ pháp tuyến là \(\overrightarrow {{n_3}} = \left( {1; - 1} \right)\) và đi qua điểm \(A(1;1)\), suy ra ta có phương trình tổng quát của đường thẳng AC là:
\(\left( {x - 1} \right) - \left( {y - 1} \right) = 0 \Leftrightarrow x - y = 0\)
Độ dài đường cao kẻ từ B chính là khoảng cách từ điểm B đến đường thẳng AC
\(d\left( {B,AC} \right) = \frac{{\left| {5 - 2} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \frac{{3\sqrt 2 }}{2}\)
CM
11 tháng 3 2017
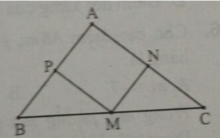
Tam giác ABC có M; N ; P lần lượt là trung điểm của BC; AC ; BC nên PM và MN là đường trung bình của tam giác ABC.
Suy ra: PM// AC; NM // AB.
Do đó, tứ giác ANMP là hình bình hành.
1 hehe