Giả sử chiều dài của hai đoạn thẳng có giá trị đo được lần lượt là a = 51 ± 1 cm và b = 49 ± 1 cm. Trong các đại lượng được tính theo các cách sau đây, đại lượng nào có sai số tương đối lớn nhất:
A. a + b
B. a – b
C. a x b
D. \(\dfrac{a}{b}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
9 tháng 12 2023
A. a + b có F = a + b
=> \(\left[ {\frac{{M.L.{T^{ - 2}}}}{{{L^2}}}} \right] = \left[ {M.{L^{ - 1}}.{T^{ - 2}}} \right]\)
B. a – b có F = a – b
=> \(\delta F = \frac{{\Delta F}}{{\overline F }} = \frac{{\Delta a + \Delta b}}{{\overline a - \overline b }} = \frac{{1 + 1}}{{51 - 49}} = 1\)
C. a x b, có F = a x b
=> \(\delta F = \delta a + \delta b = \frac{{\Delta a}}{{\overline a }} + \frac{{\Delta b}}{{\overline b }} = \frac{1}{{51}} + \frac{1}{{49}} \approx 0,04\)
D. Có F = a/b
=> \(\delta F = \delta a + \delta b = \frac{{\Delta a}}{{\overline a }} + \frac{{\Delta b}}{{\overline b }} = \frac{1}{{51}} + \frac{1}{{49}} \approx 0,04\)
Chọn B.
VT
9 tháng 4 2017
Đáp án D
Phương pháp: Sư du ̣ng công thưc tinh sai số
Cách giải:
Sai số tương đối của pháp đo U là:
VT
26 tháng 5 2017
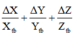
Giải thích: Đáp án D
Phương pháp:
Sử dụng lí thuyết về khoảng cách của hai vật dao động điều hoà
Khảo sát hàm số bậc hai
Cách giải:
Phương trình dao động của vật A là 
Phương trình dao động của vật B là 
Mặt khác: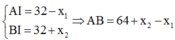 
Có:
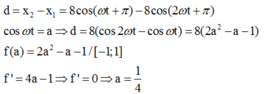
Xét bảng biến thiên sau:
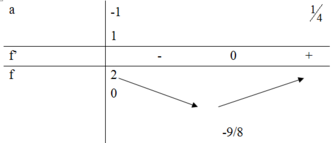
Từ bảng biến thiên ta có:
VT
2 tháng 9 2019
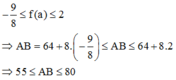
Đáp án D
Chọn chiều dương như trong hình vẽ, O1 và O2 là VTCB của A và B, quỹ đạo được biểu thị bằng các điểm M,N,P,Q như trong hình (quỹ đạo của A là đoạn M N = 16 c m ; của B là đoạn P Q = 16 c m ). Có O là gốc tọa độ.
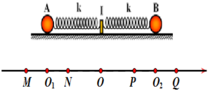
Ban đầu A dãn 8 cm nên ở vị trí M, B nén 8 cm nên ở vị trí P. Suy ra có phương trình dao động:
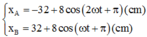
Khoảng cách AB:
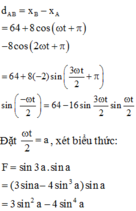
Đây là dạng tam thức bậc 2.
VT
28 tháng 10 2017
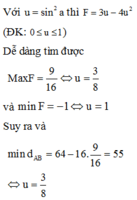
Đáp án D
Chọn hệ trục tọa độ như hình vẽ
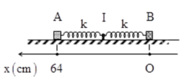
Phương trình dao động của mỗi vật
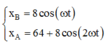
Khoảng cách giữa hai vật
Biến đổi lượng giác
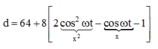
Khảo sát hàm số ta thu được
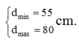
Giả sử chiều dài của hai đoạn thẳng có giá trị đo được lần lượt là a = 51 ± 1 cm và b = 49 ± 1 cm. Trong các đại lượng được tính theo các cách sau đây, đại lượng nào có sai số tương đối lớn nhất:
A. a + b
B. a – b
C. a x b
D. \(\dfrac{a}{b}\)