Phân tích đa thức thành nhân tử A. 4x^2-12xy+9y^2-8x+12y B. 3x^2+20x-7 C. (3x-1)^4+2(9y^2-6x+1)+1 D. 2x^3-3x^2+2x-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 7 2021
a) Ta có: \(\left(4x^2-3x-18\right)^2-\left(4x^2+3x\right)^2\)
\(=\left(4x^2-3x-18-4x^2-3x\right)\left(4x^2-3x-18+4x^2+3x\right)\)
\(=\left(-6x-18\right)\left(8x^2-18\right)\)
\(=-6\left(x+3\right)\cdot2\left(4x^2-9\right)\)
\(=-12\left(x+3\right)\left(2x-3\right)\left(2x+3\right)\)
b) Ta có: \(9\left(x+y-1\right)^2-4\left(2x+3y+1\right)^2\)
\(=\left(3x+3y-3\right)^2-\left(4x+6y+2\right)^2\)
\(=\left(3x+3y-3-4x-6y-2\right)\left(3x+3y-3+4x+6y+2\right)\)
\(=-\left(x+3y+5\right)\left(7x+9y-1\right)\)
25 tháng 7 2021
c) Ta có: \(-4x^2+12xy-9y^2+25\)
\(=-\left(4x^2-12xy+9y^2-25\right)\)
\(=-\left[\left(2x-3y\right)^2-25\right]\)
\(=-\left(2x-3y-5\right)\left(2x-3y+5\right)\)
d) Ta có: \(x^2-2xy+y^2-4m^2+4mn-n^2\)
\(=\left(x^2-2xy+y^2\right)-\left(4m^2-4mn+n^2\right)\)
\(=\left(x-y\right)^2-\left(2m-n\right)^2\)
\(=\left(x-y-2m+n\right)\left(x-y+2m-n\right)\)
CC
1
23 tháng 9 2021
a: \(ab+a+b+1\)
\(=a\left(b+1\right)+\left(b+1\right)\)
\(=\left(b+1\right)\left(a+1\right)\)
c: \(4x^2-12xy+3x-9y\)
\(=4x\left(x-3y\right)+3\left(x-3y\right)\)
\(=\left(x-3y\right)\left(4x+3\right)\)
20 tháng 10 2021
b: \(x^2-6x+xy-6y\)
\(=x\left(x-6\right)+y\left(x-6\right)\)
\(=\left(x-6\right)\left(x+y\right)\)
c: \(2x^2+2xy-x-y\)
\(=2x\left(x+y\right)-\left(x+y\right)\)
\(=\left(x+y\right)\left(2x-1\right)\)
e: \(x^3-3x^2+3x-1=\left(x-1\right)^3\)
TL
20 tháng 8 2021
a) \(3xy-6xy^2=3xy\left(1-2y\right)\)
b) \(3x^3+6x^2+3x=3x\left(x^2+2x+1\right)=3x\left(x+1\right)^2\)
c) \(x^3-x^2+2\)
d) \(x^2+4x+4-y^2=\left(x^2+4x+4\right)-y^2=\left(x+2\right)^2-y^2=\left(x-y+2\right)\left(x+y+2\right)\)
e) \(x^3+4x^2+4x=x\left(x^2+4x+4\right)=x\left(x+2\right)^2\)
f) \(x^2+2x+1-9y^2=\left(x+1\right)^2-\left(3y\right)^2=\left(x-3y+1\right)\left(x+3y+1\right)\)
g) \(6x^2-12x=6x\left(x-2\right)\)
h) \(x^3-2x^2+x=x\left(x^2-2x+1\right)=x\left(x-1\right)^2\)
i) \(x^2-2xy+y^2-9=\left(x-y\right)^2-3^2=\left(x-y-3\right)\left(x-y+3\right)\)
20 tháng 8 2016
2/ (b4 - 4b2 + 4) - 9a2 = (b2 - 2)2 - 9a2 = (b2 - 2 + 3a)(b2 - 2 - 3a)
2 tháng 8 2017
a)
\(4x^2-9y^2+6x-9y=\left(2x-3y\right)\left(2x+3\right)+3\left(2x-3y\right)\)
\(=\left(2x-3y\right)\left(2x+3y+3\right)\)
b)
\(1-2x+2yz+x^2-y^2-z^2=\left(x^2-2x+1\right)-\left(y^2-2yz+z^2\right)\) (đổi dấu)
\(=\left(x-1\right)^2-\left(y-z\right)^2\)
c)
\(x^3-1+5x^2-5+3x-3=\left(x-1\right)\left(x^2+x+1\right)+5\left(x-1\right)\left(x+1\right)+3\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+x+1+5\left(x+1\right)+3\right)\)
\(=\left(x-1\right)\left(x^2+x+1+5x+5+3\right)\)
\(=\left(x-1\right)\left(x^2+6x+9\right)=\left(x-1\right)\left(x+3\right)^2\)
RM
2 tháng 9 2018
\(x^2+4x-y^2+4\)
\(=\left(x^2+4x+4\right)-y^2\)
\(=\left(x^2+2\right)^2-y^4\)
\(=\left(x^2+y^2+2\right)\left(x^2-y^2+2\right)\)
16 tháng 9 2018
\(\left(x^2+4x+4\right)-y^2\)
\(=\left(x+2\right)^2-y^2\)
\(=\left(x+2+y\right)\left(x+2-y\right)\)
.
hk tôt
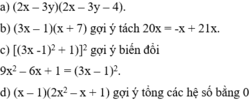
a: =(2x-3y)^2-4(2x-3y)
=(2x-3y)(2x-3y-4)
b: =3x^2+21x-x-7
=(x+7)(3x-1)
c: =(3x-1)^4+2(3x-1)^2+1
=[(3x-1)^2+1]^2
d: =2x^3-2x^2-x^2+x+x-1
=(x-1)(2x^2-x+1)