Tìm các chữ số a,b để số a4870b chia hết cho cả 2;5 và 9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Dấu hiệu chia hết cho 5 : các chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5
Vậy b có thể bằng 0 hoặc 5
Dấu hiệu chia hết cho 9 : tổng các chữ số đó cộng lại chia hết cho 9 thì số đó chia hết cho 9
4 + 8 + 7 + 0 = 19 ( ko chia hết cho 9 )
Vậy a chỉ có thể bằng 8
Vậy b = 0
Số cần tìm là 848700
Đ/s : 848700.

Dấu hiệu chia hết cho 5 : các chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5
Vậy b có thể bằng 0 hoặc 5
Dấu hiệu chia hết cho 9 : tổng các chữ số đó cộng lại chia hết cho 9 thì số đó chia hết cho 9
4 + 8 + 7 + 0 = 19 ( ko chia hết cho 9 )
Vậy a chỉ có thể bằng 8
Vậy b = 0
Số cần tìm là 848700
Đáp số: 848700.
Để a4870b ⋮ 5 => b ∈ { 0 ; 5 } ( do b là chữ số )
+) Với b = 0=> a4870b = a48700 , để a48700 ⋮ 9 => a + 4 + 8 + 7 + 0 + 0 ⋮ 9
=> 19 + a ⋮ 9 => a = 8 ( do a là chữ số )
+) Với b = 5 => a4870b = a48705 , để a48705 ⋮ 9 => a + 4 + 8 + 7 + 0 + 5 ⋮ 9
=> 24 + a ⋮ 9 => a = 3 ( do a là chữ số )
Vậy a = 8 <=> b = 0
a = 3 <=> b = 5
~~Học tốt~~

a: Đặt \(A=\overline{2a3b}\)
A chia hết cho2 và 5 khi A chia hết cho 10
=>b=0
=>\(A=\overline{2a30}\)
A chia hết cho 9
=>2+a+3+0 chia hết cho 9
=>a+5 chia hết cho 9
=>a=4
Vậy: \(A=2430\)
b: \(42=2\cdot3\cdot7;54=3^3\cdot2\)
=>\(ƯCLN\left(42;54\right)=2\cdot3=6\)
=>\(ƯC\left(42;54\right)=\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
c: \(n+4⋮n+1\)
=>\(n+1+3⋮n+1\)
=>\(3⋮n+1\)
=>\(n+1\in\left\{1;-1;3;-3\right\}\)
=>\(n\in\left\{0;-2;2;-4\right\}\)
mà n là số tự nhiên
nên \(n\in\left\{0;2\right\}\)
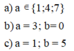

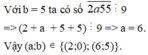


Dấu hiệu chia hết cho 5 : các chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5
Vậy b có thể bằng 0 hoặc 5
Dấu hiệu chia hết cho 9 : tổng các chữ số đó cộng lại chia hết cho 9 thì số đó chia hết cho 9
4 + 8 + 7 + 0 = 19 ( ko chia hết cho 9 )
Vậy a chỉ có thể bằng 8
Vậy b = 0
b = 0 cũng chia hết cho 2
Số cần tìm là 848700
Những số chia hết cho \(2\) và \(5\) là những số có tận cùng là những số có tận cùng là \(0\) vì \(2\times5=10\) và những số chia hết cho \(10\) là những số có tận cùng là \(0\)
Từ đó ta dễ biết \(b=0\)
Ta có: \(\overline{a48700}=a+4+8+7+0+0=19\)
Ma những số chia hết cho \(9\) là những số có tổng các chữ số chia hết cho \(9\)
Mà \(27\) chia hết cho \(9\) nên \(a=27-19=8\)
Vậy \(a=8\)
Vậy số \(\overline{a4870b}=848700\) để chia hết cho \(2;5\) và \(9\)