Cho a+b+c=0. Cmr ab+bc+ac \(\le\)0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Vế đầu:
Áp dụng BĐT AM-GM:
$(ab+bc+ac)(a+b+c)\geq 9abc$
$\Leftrightarrow ab+bc+ac\geq 9abc$
$\Rightarrow ab+bc+ac-2abc\geq 9abc-2abc=7abc\geq 0$ do $a,b,c\geq 0$
Vế sau:
Áp dụng BĐT Schur:
$abc\geq (a+b-c)(b+c-a)(c+a-b)=(1-2a)(1-2b)(1-2c)$
$\Leftrightarrow 9abc\geq 4(ab+bc+ac)-1$
$\Rightarrow 2abc\geq \frac{8}{9}(ab+bc+ac)-\frac{2}{9}$
$\Rightarrow ab+bc+ac-2abc\leq ab+bc+ac-[\frac{8}{9}(ab+bc+ac)-\frac{2}{9}]=\frac{ab+bc+ac}{9}+\frac{2}{9}$
$\leq \frac{(a+b+c)^2}{27}+\frac{2}{9}$ (theo BĐT AM-GM)
$=\frac{1}{27}+\frac{2}{9}=\frac{7}{27}$
Ta có đpcm.

a.
\(\sum\dfrac{ab}{a+c+b+c}\le\dfrac{1}{4}\sum\left(\dfrac{ab}{a+c}+\dfrac{ab}{b+c}\right)=\dfrac{a+b+c}{4}\)
2.
\(\dfrac{ab}{a+3b+2c}=\dfrac{ab}{a+b+2c+2b}\le\dfrac{ab}{9}\left(\dfrac{4}{a+b+2c}+\dfrac{1}{2b}\right)=4.\dfrac{ab}{a+b+2c}+\dfrac{a}{18}\)
Quay lại câu a
cho ba số dương \(0\le a\le b\le c\le1\) CMR \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le2\)

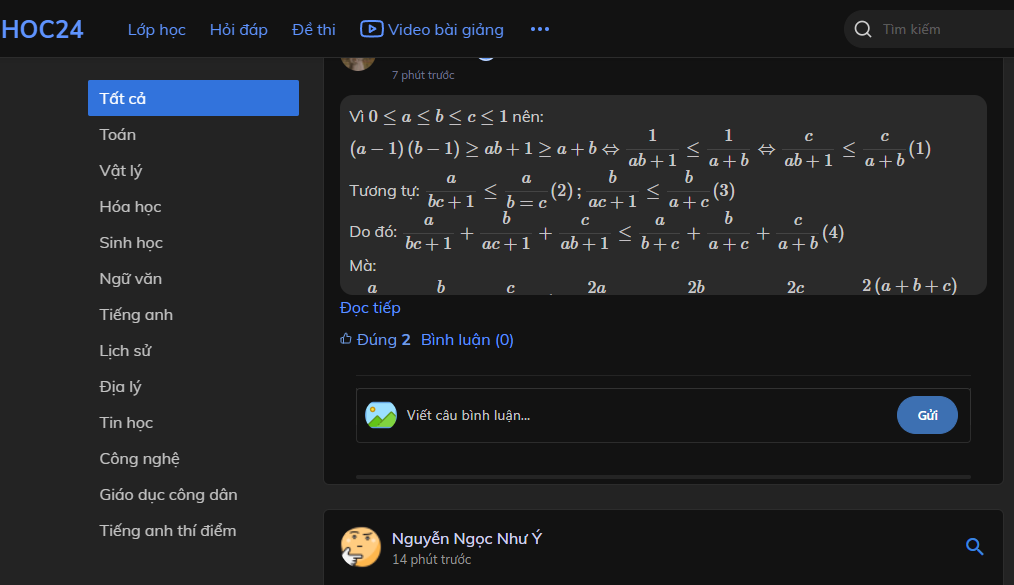
Vì \(0\le a\le b\le c\le1\) nên:
\(\left(a-1\right)\left(b-1\right)\ge ab+1\ge a+b\Leftrightarrow\dfrac{1}{ab+1}\le\dfrac{1}{a+b}\Leftrightarrow\dfrac{c}{ab+1}\le\dfrac{c}{a+b}\left(1\right)\)
Tương tự: \(\dfrac{a}{bc+1}\le\dfrac{a}{b=c}\left(2\right);\dfrac{b}{ac+1}\le\dfrac{b}{a+c}\left(3\right)\)
Do đó: \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\left(4\right)\)
Mà: \(\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\le\dfrac{2a}{a+b+c}+\dfrac{2b}{a+b+c}+\dfrac{2c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\left(5\right)\)
Từ (4) và (5) suy ra \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\left(đpcm\right)\)

Áp dụng bđt cosi ta có:
`a+b>=2sqrt{ab}`
`=>(ab)/(a+b)<=(sqrt{ab})/2`
Chứng minh tt:
`(bc)/(b+c)<=(sqrt{bc})/2`
`(ca)/(a+c)<=(sqrt{ca})/2`
`=>VT<=(sqrt{ab}+sqrt{bc}+sqrt{ca})/2`
Áp dụng cosi:
`sqrt{ab}<=(a+b)/2`
`sqrt{bc}<=(b+c)/2`
`sqrt{ca}<=(c+a)/2`
`=>(sqrt{ab}+sqrt{bc}+sqrt{ca})/2<=(a+b+c)/2`
`=>VT<=(a+b+c)/2`


Ta có:\(\sqrt{\frac{bc}{a+bc}}=\sqrt{\frac{bc}{a\left(a+b\right)+c\left(a+b\right)}}\)
\(=\sqrt{\frac{bc}{\left(a+b\right)\left(a+c\right)}}\le\frac{1}{2}\left(\frac{b}{a+b}+\frac{c}{a+c}\right)\) (Áp dụng BĐT AM-GM)
Tương tự với hai BĐT còn lại và cộng theo vế ta thu được đpcm.