Cho hình vẽ bên, hãy tính tỉ số giữa diện tích hình tròn bé và diện tích hình tròn lớn.l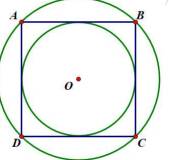
Làm nhanh giúp mik ai làm đầu tiên mik cho tik
11/1 lúc 16:00 mik phải nộp rồi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
Đoàn Đức Hà
Giáo viên
11 tháng 1 2023
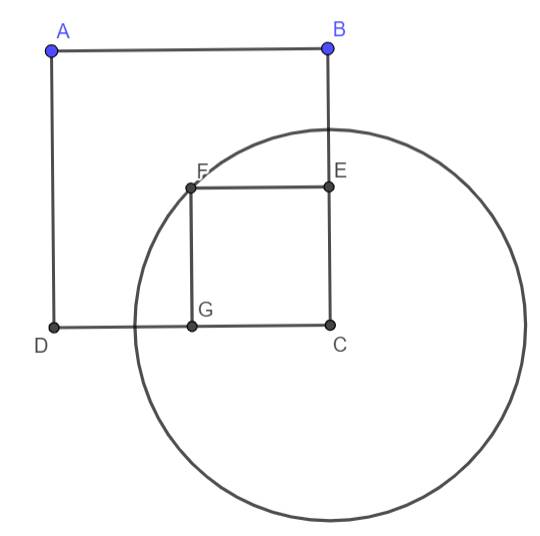
Diện tích của phần gạch sọc là diện tích của \(8\) hình lá nhỏ.
Diện tích \(2\) hình lá nhỏ (mô tả như hình vẽ trên) là hiệu của \(\dfrac{1}{4}\) diện tích hình tròn trừ đi diện tích hình vuông \(CEFG\).
Do đó diện tích của \(8\) hình lá nhỏ (tức diện tích phần gạch sọc) là diện tích của hình tròn trừ đi diện tích hình vuông \(ABCD\).
Diện tích hình tròn là: \(S_1=3,14\times CF\times CF=3,14\times\dfrac{CA}{2}\times\dfrac{CA}{2}=0,785\times CA\times CA\)
Diện tích hình vuông \(ABCD\) là: \(S_2=8\times8=64\left(cm^2\right)\)
Mà ta cũng có thể tính diện tích hình vuông \(ABCD\) bằng cách:
\(S_2=\dfrac{AC\times BD}{2}=\dfrac{AC\times AC}{2}\)
Suy ra \(AC\times AC=64\times2=128\)
Diện tích phần gạch sọc là:
\(S_1-S_2=0,785\times AC\times AC-\dfrac{AC\times AC}{2}=0,285\times AC\times AC=36,48\left(cm^2\right)\)
DD
Đoàn Đức Hà
Giáo viên
11 tháng 1 2023
Gợi ý: Cắt ghép hình ta được diện tích một lá mầm là diện tích của \(\dfrac{1}{4}\) hình tròn trừ đi diện tích của tam giác vuông.
LH
0
1 tháng 2 2016
Bán kính hình tròn thứ 2 là :
8 : 2 = 4 ( cm )
a) . DT hình tròn thứ nhất là :
8 x 8 x 3.14 = 200.96 ( cm2 )
DT hình tròn thứ hai là :
4 x 4 x 3.14 = 50.24 ( cm2 )
b) . Tỉ số % giũa hình tròn thứ 2 với hình tròn thứ 1 là :
50.24 : 200.96 = 0.25 = 25 %
Đ/S : a) : Hình tròn 1 : 200.96 cm2
Hình tròn 2 : 50.24 cm2
b) 25 %
I
22 tháng 2 2020
bài 1 )diện tích hình tròn là
50x3,14=157 cm2
diệ tích hình chữ nhật là
157:100x18%=28.26cm2
diện tích phần còn lại là
157-28.26=128.74cm2
bài 2 ko hình sao làm
Diện tích hình tròn lớn là: \(S_1=3,14\times OC\times OC\)
Diện tích hình tròn bé là: \(S_2=3,14\times OP\times OP\)
Tỉ số diện tích hình tròn bé và hình tròn lớn là:
\(\dfrac{S_2}{S_1}=\dfrac{3,14\times OP\times OP}{3,14\times OC\times OC}=\dfrac{OP\times OP}{OC\times OC}\)
\(=\dfrac{\left(\dfrac{1}{2}\times MP\right)\times\left(\dfrac{1}{2}\times MP\right)}{\left(\dfrac{1}{2}\times AC\right)\times\left(\dfrac{1}{2}\times AC\right)}=\dfrac{MP\times MP}{AC\times AC}\)
\(=\dfrac{AB\times BC}{AC\times BD}=\dfrac{S_{ABCD}}{2\times S_{ABCD}}=\dfrac{1}{2}\).