Cho tam giác ABC vuông cân tại A, M là điểm nằm trên cạnh BC (M khác B, C). Vẽ M, E lần lượt vuông góc với AB, AC tại E và F. Trên tia MF lấy I sao cho MI = AB
a) Tứ giác ABMI; AEMF là hình gì? Vì sao?
b) Giả sử BC= 8cm. Tính diện tích tam giác ABC.
c) Gọi D là điểm đối xứng với A qua BC. Chứng minh AB = CD và BF I DE
d) Chứng minh các đường thẳng DM, BF, CE đồng quy Mình cần gấp câu c, d ạ

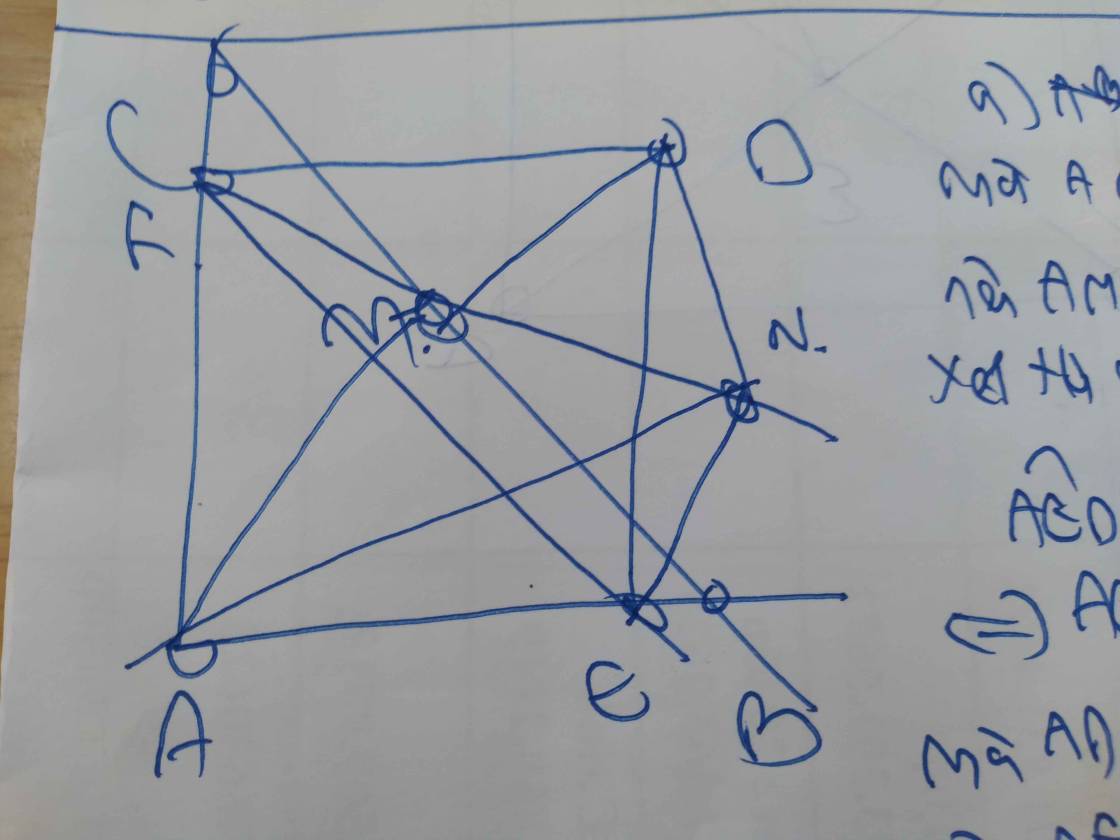


a: Xét tứ giác ABMI có
MI//AB
MI=AB
Do đó; ABMI là hình bình hành
Xét tứ giác AEMF có
góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hìnhchữ nhật
b: \(AB=\sqrt{\dfrac{BC^2}{2}}=\sqrt{32}=4\sqrt{2}\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot4\sqrt{2}\cdot4\sqrt{2}=2\sqrt{2}\cdot4\sqrt{2}=16\left(cm^2\right)\)
c: A đối xứng D qua BC
nên CA=CD
=>CD=AB