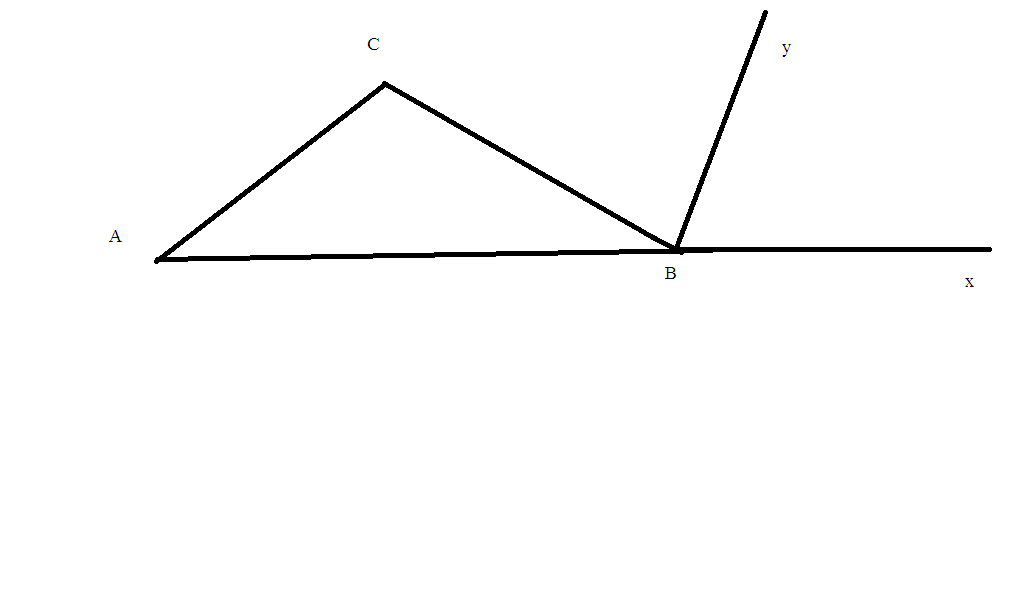
Vẽ tam giác ABC. Có góc A=50 độ, góc B=80 độ. Kẻ Bx là tia đối của tia Ba và tia By là tia phân giác của góc CBx. Chứng tỏ rằng By song song với AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : HCK = HBC (cùng phụ với ^BKC) (1)
HCB+HBC=90* (hai góc nhọn trong tam giác vuông)
BCA+CBA=90* (hai góc nhọn trong tam giác vuông)
Nên HCB+HBC+BCA+CBA=90+90*=180*
Hay HCA+HBA=180*
Mà HBx + HBA=180* (hai góc kề bù)
Do đó HCA=^HBx (2)
Mà HBC=^HBx (do By là phân giác) (3)
Vay từ (1), (2), (3) suy ra HCK = HCA (đpcm)

Xét ΔABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(Định lí tổng ba góc của một tam giác)
=>\(100^o+40^o+\widehat{A}=180^O\)
\(\Rightarrow\widehat{A}=40^o\)
a)Xét ΔABC có \(\widehat{xBC}\) là góc ngoài tam giác ABC tại đỉnh B, ta có:
\(\widehat{xBC}=\widehat{C}+\widehat{A}\)
\(\Rightarrow\widehat{xBC}=40^o+100^o=140^o\)
b)Chứng minh // thì đc chứ ⊥ thì, xem lại đề nhé bn

Ta có : HCK = HBC ( cùng phụ với BKC) (1)
HCB + HBC = 90° ( tổng các góc trong ∆)
BCA + CBA = 90° ( tổng các góc trong ∆)
=> HCB + HBC + BCA + CBA = 180°
Hay HCA + HBA = 180°
Mà HBx + HBA = 180° ( kề bù)
Do đó : HCA = HBx (2)
Mà HBC = HBx ( By là phân giác) (3)
Từ (1)(2)(3) => HCK = HCA
Ta có : HCK = HBC ( cùng phụ với BKC) (1)
HCB + HBC = 90° ( tổng các góc trong ∆)
BCA + CBA = 90° ( tổng các góc trong ∆)
=> HCB + HBC + BCA + CBA = 180°
Hay HCA + HBA = 180°
Mà HBx + HBA = 180° ( kề bù)
Do đó : HCA = HBx (2)
Mà HBC = HBx ( By là phân giác) (3)
Từ (1)(2)(3) => HCK = HCA
Góc xBC là góc ngoài của tam giác ABC tại đỉnh B
=> góc xBC + CBA = 180o
=> xBC = 180o - CBA = 180o - 80o = 100o
Mà By là tia p/g của góc xBC nên góc xBy = 1/2. xBC = 1/2 . 100o = 50o = góc BAC
Mà 2 góc này ở vị trí đồng vị nên By // AC