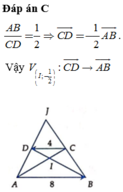cho hình thang ABCD ( AB//CD) I là giao điểm hai đường chéo . Gọi S1là SABC,S2là SAID .Tính S hình thang theo S1và S2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
4 tháng 4 2021
Ta thấy tam giác ACD và tam giác BCD có chung đáy cd , chiều cao bằng nhau và bằng chiều cao hình thang ABCD . Nên Sacd=Sbcd. Suy ra Saod=Sboc
b) cho diện tích abo=a thì chắc mình mới làm được nhé....
Xét tam giác aob và cod có
aob=cod (đối đỉnh), abo=cdo(so le trong do ab//cd)
Suy ra 2 tam giác này đồng dạng
=> (Ao/oc)^2=Saob/Scod=a/b
Xét tam giác aod và cdo chung đường cao hạ từ d xuống ac. Suy ra Saod/Scod=ao/co= căn (a/b)
=> Saod= căn (a/b) * b= căn (ab)
KC
9 tháng 4 2021
Kết quả đúng ạ mà mik có cách ngắn hơn rồi, cảm ơn bạn đã giúp ạ😄
CM
26 tháng 4 2017
Đáp án C
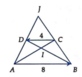
A B C D = 1 2 ⇒ C D → = − 1 2 A B → . Vậy V I ; − 1 2 : C D → → A B →
21 tháng 6 2022
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD
21 tháng 6 2022
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD
GH
22 tháng 6 2023
2)
Có: \(\left\{{}\begin{matrix}AB=AD\left(gt\right)\\AD=BC\left(2.cạnh.bên.hình.thang.cân\right)\end{matrix}\right.\)
\(\Rightarrow AB=BC\Rightarrow\Delta ABC.cân.tại.B\)
Mà AB // ED (gt)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\left(so.le.trong\right)\)
\(\Rightarrow\widehat{ACB}=\widehat{ACD}\)
=> CA là tia phân giác của góc C.
CM
2 tháng 6 2018
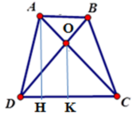
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang: AH = 2 S A B C D A B + C D = 2.48 4 + 8 = 8 (cm)
Vì AB // CD (do ABCD là hình thang) nên theo định lý Ta-lét ta có
O C O A = C D A B = 8 4 = 2 ⇒ O C O A + O C = 2 2 + 1 ⇒ O C A C = 2 3
Vì AH // OK (cmt) nên theo định lý Ta-lét cho tam giác AHC ta có:
O K A H = O C A C = 2 3 => OK = 2 3 AH => OK = 2 3 .6 = 4(cm)
Do đó S C O D = 1 2 OK.DC = 1 2 . 16 3 .8 = 64 3 c m 2
Đáp án: A
CM
12 tháng 5 2017
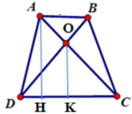
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang: AH = 2 S A B C D A B + C D = 2.36 4 + 8 = 6 (cm)
Vì AB // CD (do ABCD là hình thang) nên theo định lý Ta-lét ta có
O C O A = C D A B = 8 4 = 2 ⇒ O C O A + O C = 2 2 + 1 ⇒ O C A C = 2 3
Vì AH // OK (cmt) nên theo định lý Ta-lét cho tam giác AHC ta có:
O K A H = O C A C = 2 3 => OK = 2 3 AH => OK = 2 3 .6 = 4(cm)
Do đó S C O D = 1 2 OK.DC = 1 2 .4.8 = 16cm2
Đáp án: C