Một người gọi điện thoại nhưng quen hai chữ số cuối mà chỉ nhớ hai chữ số đó Người đó bẩm ngẫu nhiên hai số cuối. Xác suất để người đó gọi đúng số là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 8 2017
Chọn B
Gọi Ω là tập hợp tất cả các cách chọn 2 số phân biệt trong 10 chữ số 0,1,2,3,…9
Khi đó n(Ω)=90. Gọi A là biến cố “trong một lần gọi”
Ta có n(A)=1 => P ( A ) = 1 90
CM
3 tháng 12 2019
Chọn C
Có 2 bộ số {a;b;c} có tổng các chữ số bằng 5 là: {0;1;4}, {0;2;3}, mỗi bộ số có 3! hoán vị nên có tất cả 12 khả năng.
Do đó xác suất để người đó bấm máy một lần đúng số cần gọi là 1 12 .
17 tháng 5 2022
Tham khảo:
Số phần tử của không gian mẫu là 
. Để người đó gọi đúng số điện thoại mà không phải thử quá hai lần ta có 2 trường hợp:
TH1: Người đó gọi đúng ở lần thứ nhất.
TH2: Người đó gọi đúng ở lần thứ hai. Gọi A1 người đó gọi đúng ở lần thứ nhất
Xác suất người đó gọi đúng là P(A1) = \(\dfrac{1}{10}\)
Xác suất người đó gọi không đúng là P(A1) = \(\dfrac{9}{10}\).
Gọi A2 là người đó gọi đúng ở lần thứ hai
Xác suất người đó gọi đúng là P(A2) = \(\dfrac{1}{9}\) .
Gọi A là người đó gọi đúng số điện thoại mà không phải thử quá hai lần, ta có 
(đpcm)
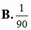
n(A)=1
\(n\left(\Omega\right)=C^1_{10}\cdot C^1_9=90\)
=>Xác suất đúng là 1/90