tìm tất cả cách giá trị nguyên của x để 2x^2-x+1 chia hết cho 2x+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ x khac -1\(A=\frac{x^3+2x^2-1}{x^3+2x^2+2x+1}=\frac{x^3+x^2+x^2+x-x-1}{x^3+x^2+x^2+x+x+1}=\frac{x^2\left(x+1\right)+x\left(x+1\right)-\left(x+1\right)}{x^2\left(x+1\right)+x\left(x+1\right)+\left(x+1\right)}=\frac{\left(x+1\right)\left(x^2+x-1\right)}{\left(x+1\right)\left(x^2+x+1\right)}=\frac{x^2+x-1}{x^2+x+1}\)
\(ta.coA=\frac{x^2+x-1}{x^2+x+1}=\frac{x^2+x+1-2}{x^2+x+1}=1-\frac{2}{x^2+x+1}\)
Để A \(\in Z\Leftrightarrow\frac{2}{x^2+x+1}\in Z\Rightarrow x^2+x+1\inƯ\left(2\right)\Rightarrow\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\in\left\{\pm1;\pm2\right\}\)
giải ra ta được \(x=0,x=-1\)(t/m)

Ta có P có giá trị dương=> P>0
=> (2x-1)và(5-2x) cùng dấu âm hoặc dương
Xét (2x-1)>0=>x>\(\dfrac{1}{2}\)(1)
(5-2x)>0=>x<\(\dfrac{5}{2}\) (2)
Từ (1) và (2) =>x=1 hoặc x=2
Xét (2x-1)<0=>x<\(\dfrac{1}{2}\)(3)
(5x-2)<0=>x>\(\dfrac{5}{2}\)(4)
Từ (3) và (4) => x ko có giá trị nào
Vậy x=1 hoặc x=2

2x2+3x+2=2x2+2x+x+2=2x(x+1)+(x+2)
Vì 2x(x+1) chia hết cho x+1
=> x+2 chia hết cho x+1
Ta có: x+2=x+1+1
x nguyên => x+1 nguyên => x+1 thuộc Ư (1)={-1;1}
Với x+1=1 => x=0
Với x+1=-1 => x=-2
Vậy x={0;-2} thì 2x2+3x+2 chia hết cho x+1
Ta có : 2.x2+3x+2 \(⋮\)x+1
=) [ 2.x2+3x+2 - ( x + 1 ) ] \(⋮\)x+1
=) [ 2.x2+3x+2 - 3( x + 1 ) ] \(⋮\)x+1
=) [ 2.x2+3x+2 - (3x + 3 ) ] \(⋮\)x+1
=) 2.x2+3x+2 - 3x - 3 \(⋮\)x+1

\(2x^2+3x+2⋮x+1\)
\(\Rightarrow2x^2+2x+x+2⋮x+1\)
\(\Rightarrow2x\left(x+1\right)+\left(x+1\right)+1⋮x+1\)
\(\Rightarrow1⋮x+1\)\(\Rightarrow x+1\inƯ\left(1\right)=\left\{\pm1\right\}\)
\(\Rightarrow\hept{\begin{cases}x+1=1\\x+1=-1\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=0\\x=-2\end{cases}}\)
2x2+3x+2=2x2+2x+x+2=2x(x+1)+(x+2)
Vì 2x(x+1) chia hết cho x+1
=> x+2 chia hết cho x+1
Ta có: x+2=x+1+1
x nguyên => x+1 nguyên => x+1 thuộc Ư (1)={-1;1}
Với x+1=1 => x=0
Với x+1=-1 => x=-2
Vậy x={0;-2} thì 2x2+3x+2 chia hết cho x+1

Ta có : \(2x^2+3x+2=\left(2x^2+2x\right)+\left(x+1\right)+1\)
\(=2x\left(x+1\right)+\left(x+1\right)+1=\left(x+1\right)\left(2x+1\right)+1\)
Để \(\left(2x^2+3x+2\right)⋮\left(x+1\right)\)
thì \(1⋮x+1\) hay \(x+1\inƯ\left(1\right)\)
\(\Rightarrow x+1\in\left\{-1,1\right\}\)
\(\Leftrightarrow x\in\left\{-2,0\right\}\)
Vậy : \(x\in\left\{-2,0\right\}\) để \(\left(2x^2+3x+2\right)⋮\left(x+1\right)\)
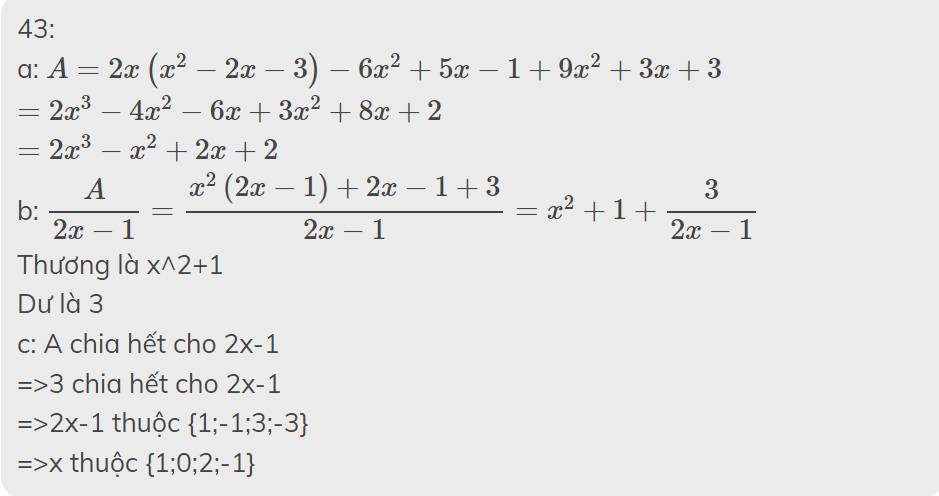
=>2x^2+x-2x-1+2 chia hết cho 2x+1
=>\(2x+1\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{0;-1\right\}\)