MN ơi giúp em với ;-; "Khi cộng hai số thập phân một bạn đã viết nhầm dấu phẩy của một số hạng sang bên phải một chữ số do đó dẫn đến kết quả sai là 226,5 Em hãy tìm hai số ban đầu biết kết quả đúng của phép cộng trên là 89,25
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 8 2021
5, chắc đồng chất cùng S
\(=>\dfrac{R1}{R2}=\dfrac{l1}{l2}=>\dfrac{l1}{l2}=\dfrac{6R2}{R2}=6=>l1=6R2\)
=>chiều dài dây 1 lớn hơn và gấp 6 lần dây 2
b,\(=>\dfrac{l1}{l2}=6=>\dfrac{l1}{35-l1}=6=>l1=30m=>l2=5m\)
6\(=>\),\(l1=4l2\),
\(=>\dfrac{R1}{R2}=\dfrac{\dfrac{pl1}{S1}}{\dfrac{pl2}{S2}}=\dfrac{l1}{l2}=4=>R1=4R2=>R1>R2\)
\(=>\dfrac{U}{R1}< \dfrac{U}{R2}=>I1< I2\)=>dd qua dây 1 nhỏ hơn qua dây2
7, \(=>\dfrac{R1}{R2}=\dfrac{l1}{l2}=\dfrac{3}{2}=1,5=>R1=1,5R2\)
\(=>\left(1-R2\right)=1,5R2=>R2=0,4\Omega=>R1=0,6\Omega\)
M
0
A
0
M
1
17 tháng 1 2022
a: 2+5/6=12/6+5/6=17/6
b: 5/12+3/4+1/3=5/12+9/12+4/12=18/12=3/2
c: 2/3+3/4=8/12+9/12=17/12
IN
0
27 tháng 8 2021
\(=>\dfrac{R1}{R2}=\dfrac{l1}{l2}=>\dfrac{20}{R2}=\dfrac{3}{6}=>R2=\dfrac{20.6}{3}=40\Omega\)
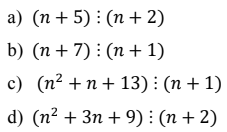
Lời giải:
Gọi 2 số cần tìm là a và b, số bị viết nhầm là b. Khi b bị lệch dấu phẩy sang phải 1 chữ số thì số mới gấp 10 lần số b. Ta có:
$a+b=89,25$ (1)
$a+10\times b=226,5$ (2)
Lấy phép tính (2) trừ (1) theo vế thu được:
$10\times b-b=226,5-89,25$
$9\times b=137,25$
$b=137,25:9=15,25$
$a=89,25-15,25=74$
Vậy 2 số cần tìm là $74$ và $15,25$