Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
Xét hai tam giác vuông ABE và ADH:
\(AD=AB\)
\(\widehat{BAE}=\widehat{DAH}\) (cùng phụ \(\widehat{DAE}\))
\(\Rightarrow\Delta_vABE=\Delta_vADH\) (góc nhọn-cạnh góc vuông) (1)
\(\Rightarrow AH=AE\)
\(\Rightarrow\Delta AHE\) vuông cân tại A
b. Cũng từ (1) ta có \(BE=DH\)
Xét hai tam giác vuông ABE và FDA có:
\(\widehat{BAE}=\widehat{AFD}\) (so le trong)
\(\Rightarrow\Delta_vABE\sim\Delta_vFDA\)
\(\Rightarrow\dfrac{AB}{DF}=\dfrac{BE}{AD}\Rightarrow AB.AD=BE.DF\Rightarrow AB^2=HD.DF\) (do AD=AB và BE=HD)
c. Ta có: \(\left\{{}\begin{matrix}S_{HAF}=\dfrac{1}{2}AH.AF\\S_{HAF}=\dfrac{1}{2}AD.HF\end{matrix}\right.\) \(\Rightarrow AH.AF=AD.HF\)
\(\Rightarrow\dfrac{1}{AD}=\dfrac{HF}{AH.AF}\Rightarrow\dfrac{1}{AD^2}=\dfrac{HF^2}{AH^2.AF^2}=\dfrac{AH^2+AF^2}{AH^2.AF^2}\)
\(\Leftrightarrow\dfrac{1}{AD^2}=\dfrac{1}{AF^2}+\dfrac{1}{AH^2}=\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\) (do AH=AE theo chứng minh câu a)
\(\Leftrightarrow\dfrac{1}{AE^2}+\dfrac{1}{AF^2}=\dfrac{1}{a^2}\) cố định (đpcm)

a: Xét ΔAHB vuông tại H và ΔAHK vuông tại H có
AH chung
HB=HK
Do đó: ΔAHB=ΔAHK
b: Ta có; ΔAHB=ΔAHK
nên \(\widehat{HAK}=\widehat{BAH}\)
mà \(\widehat{BAH}=\widehat{EHA}\)
nên \(\widehat{EHA}=\widehat{HAK}\)

Lời giải:
Xét tam giác vuông $HAE$ có:
$\widehat{E}=180^0-\widehat{A}-\widehat{H}=180^0-55^0-90^0=35^0$
Xét tam giác vuông $BKE$ có:
$\widehat{KBE}+\widehat{KEB}+\widehat{BKE}=180^0$
$\widehat{KBE}=180^0-\widehat{KEB}-\widehat{BKE}=180^0-35^0-90^0=55^0$
$\widehat{HBK}=180^0-\widehat{KBE}=180^0-55^0=125^0$

cm :
góc CAK+góc BAK=góc BAC=90 độ
góc CAK+góc ACK=90 độ
=>góc BAK=góc ACK (=90 độ- góc CAK)
hay góc BAH=góc ACK
xét tam giác AHB và tam giác CKA có
góc BAH=góc ACK
AB=AC (gt)
góc AHB= góc AKC (=90 độ)
=>tam giác AHB=tam giác CKA (ch-gn)
=>HB=AK=3cm

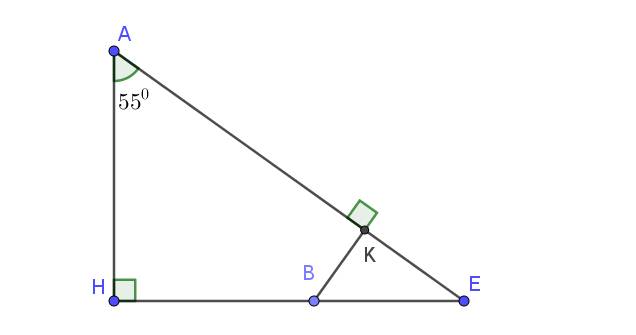
\(\Delta AHE\left(\widehat{AHE}=90^o\right):\widehat{HAE}+\widehat{HEA}=90^o\) (2 góc phụ nhau)
\(\Rightarrow\widehat{HEA}=90^o-55^o=35^o=\widehat{KEB}\)
\(\Delta KBE\left(\widehat{BKE}=90^o\right):\widehat{KBE}+\widehat{KEB}=90^o\) (2 góc phụ nhau)
\(\Rightarrow\widehat{KBE}=90^o-35^o=55^o\)
\(\widehat{KBH}+\widehat{KBE}=180^o\) (2 góc kề bù)
\(\Rightarrow\widehat{KBH}=180^o-55^o=125^o\)