Giúp mình bài này ạ, mai mình thi rồi
K
Khách
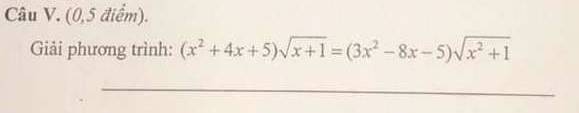
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 1 2022
a) Điện trở tương đương của đoạn mạch :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.40}{60+40}=24\left(\Omega\right)\)
b) Hiệu điện thế giữa hai đầu đoạn mạch :
\(U=I.R_{tđ}=2.24=48\left(V\right)\)
⇒ \(U=U_1=U_2=48\left(V\right)\) (vì R1 // R2)
Cường độ dòng điện chạy qua mỗi điện trở :
\(I_1=\dfrac{U_1}{R_1}=\dfrac{48}{60}=0,8\left(A\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{48}{40}=1,2\left(A\right)\)
Chúc bạn học tốt
H
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
S
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
HK
3
31 tháng 10 2021
Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi
26 tháng 6 2023
1:
a: =>(x-1)(x-7)=0
=>x=1 hoặc x=7
b: =>x(x^2-9x+8)=0
=>x(x-1)(x-8)=0
=>\(x\in\left\{0;1;8\right\}\)
c: Đặt 1/căn x-7=a; 1/căn y+6=b
Theo đề, ta có:
7a-4b=5/3 và 5a+3b=13/6
=>a=1/3 và b=1/6
=>x-7=9 và y+6=36
=>x=16 và y=30
Bài 3:
a: Δ=(2m+3)^2-4(m^2+3m+2)
=4m^2+12m+9-4m^2-12m-8=1>0
=>PT luôn có hai nghiệm pb
b: x1^2+x2^2=1
=>(x1+x2)^2-2x1x2=1
=>(2m+3)^2-2(m^2+3m+2)=1
=>4m^2+12m+9-2m^2-6m-4-1=0
=>2m^2+6m+4=0
=>m=-1 hoặc m=-2
HR
1
ĐKXĐ :\(\left\{{}\begin{matrix}x+1\ge0\\x^2+1\ge0\end{matrix}\right.\Leftrightarrow x\ge-1\)
Khi đó \((x^2+4x+5)\sqrt{x+1}=(3x^2-8x-5)\sqrt{x^2+1}\)
\(\Leftrightarrow(x^2+1)\sqrt{x+1}+4(x+1)\sqrt{x+1}=3(x^2+1)\sqrt{x^2+1}-8(x+1)\sqrt{x^2+1}\)
Đặt \(\sqrt{x+1}=a;\sqrt{x^2+1}=b(a\ge0;b>0)\)
Phương trình trở thành :
\(4a^3+ab^2=3b^3-8a^2b\)
\(\Leftrightarrow4(a^3+b^3)+b(8a^2+ab-7b^2)=0\)
\(\Leftrightarrow(a+b)(4a^2-4ab+4b^2)+(a+b)(8ab-7b^2)=0\)
\(\Leftrightarrow(a+b)(4a^2+4ab-3b^2)=0\)
\(\Leftrightarrow\left(a+b\right)\left(2a-b\right)\left(2a+3b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=0(\text{loại})\\2a-b=0\\2a+3b=0(\text{loại})\end{matrix}\right.\Leftrightarrow2a=b\) (vì \(\left\{{}\begin{matrix}a\ge0\\b>0\end{matrix}\right.\) nên a+b>0 ; 2a +3b > 0)
Trở lại cách đặt ta được
\(2\sqrt{x+1}=\sqrt{x^2+1}\Leftrightarrow x^2-4x-3=0\)
\(\Leftrightarrow x=\pm\sqrt{7}+2\) (loại \(x=-\sqrt{7}+2\))
Vậy x = \(\sqrt{7}+2\) là nghiệm phương trình