Tìm các số nguyên a, b sao cho: ab + 11 = 2a + 3b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
22 tháng 12 2022
Lời giải:
$ab+11=2a+3b$
$ab-2a-3b+11=0$
$a(b-2)-3(b-2)+5=0$
$(a-3)(b-2)=-5$
Vì $a,b$ là số nguyên nên $a-3, b-2$ là số nguyên. Ta có bảng sau: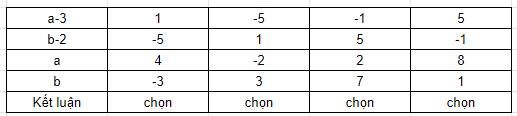
TH
3
NH
13 tháng 1 2019
a, ta có ab + 1 = 2a + 3b
\(\Leftrightarrow ab-2a-3b+6=5\)5
\(\Leftrightarrow\left(b-2\right)\left(a-3\right)=5\)
mà a , b là số nguyên tố
Nên \(\left(b-2\right)\left(a-3\right)=1.5=5.1\)
<=>b-2=1 và a-3 = 5
hoặc b -2 = 5 và a- 3 = 1
giải nốt nha
NH
5
DT
1
11 tháng 4 2020
Ta có :
2a và 6v là số chẵn mà 78 là số chẵn
=> 3b phải là số chẵn = > b là số chẵn mà b là số nguyên tố
b = 2 ( 2 là số nguyên tố chẵn duy nhất )
Ta có : 2a + 6 + 6c = 78
=> 2a + 6c = 72
=> a + 3c = 36 ( chia 2 vế cho 2 )
Ta có 36 chia hết cho 3 thì 3c chia hết cho 3
=> a phải chia hết cho 3 . Mà a là số nguyên tố
=> a = 3 ( số nguyên tố duy nhất chia hết cho 3 )
=> 3+ 3c = 36 => c = 11
= > a = 3 , b = 2 , c = 11
Chúc bạn học tốt :))
TH
1
QA
1
16 tháng 5 2016
Vì 78 chia hết cho 2 mà 2a;6c chia hết cho 2\(\Rightarrow\)3b chia hết cho 2 mà b là số nguyên tố\(\Rightarrow\)b=2
Thay b = 2 ta có:
2a+3*2 + 6c=78
2a+6+6c=78
2a+6c=78-6
2a+6c=72
Vì 72 chia hết cho 3 mà 6c chia hết cho 3\(\Rightarrow\)2a chia hết cho 3 mà a là số nguyên tố\(\Rightarrow\)a=3
Thay a=3 ta có:
2*3 + 6c=72
6+6c=72
6c=72-6
6c=66
c=66/6
c=11
Vậy a=3;b=2;c=11
NV
1
DD
Đoàn Đức Hà
Giáo viên
19 tháng 12 2020
\(2a+3b+6c=78\)
có \(2a,6c,78\)là số chẵn nên \(3b\)là số chẵn, suy ra \(b=2\).
\(\Rightarrow2a+6c=72\Leftrightarrow a+3c=36\)
có \(3c⋮3,36⋮3\)suy ra \(a⋮3\Rightarrow a=3\).
\(\Rightarrow c=\frac{36-3}{3}=11\)(thỏa mãn)
Vậy \(\left(a,b,c\right)=\left(3,2,11\right)\)
AH
Akai Haruma
Giáo viên
22 tháng 11 2021
Lời giải:
a.
$2a+3b\vdots 13$
$\Leftrightarrow 2a+13a+3b\vdots 13$
$\Leftrightarrow 15a+3b\vdots 13$
$\Leftrightarrow 3(5a+b)\vdots 13$
$\Leftrightarrow 5a+b\vdots 13$
b.
$4a+3b\vdots 11$
$\Leftrightarrow 4a-11a+3b\vdots 11$
$\Leftrightarrow -7a+3b\vdots 11$
$\Leftrightarrow -(7a-3b)\vdots 11$
$\Leftrightarrow 7a-3b\vdots 11$ (đpcm)