Giải câu 10 với câu 11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



10. Câu này chứng minh BĐT BSC:
\(\sqrt{\left(a^2+b^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ab+bc\right)^2}=b\left(a+c\right)\)
11.
Ta có: \(\dfrac{1}{1+a}+\dfrac{1}{1+b}-\dfrac{2}{1+\sqrt{ab}}\)
\(=\dfrac{\left(1+b\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{\left(1+a\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2\left(1+a\right)\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{1+b+\sqrt{ab}+b\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{1+a+\sqrt{ab}+a\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2+2a+2b+2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{-a-b+2\sqrt{ab}+a\sqrt{ab}+b\sqrt{ab}-2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{ab}-1\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\ge0\forall x,y\ge1\)
Đẳng thức xảy ra khi \(a=b=1\)



Câu 11.
a)Độ tự cảm của ống dây:
\(L=4\pi\cdot10^{-7}\cdot\dfrac{N^2}{l}S=4\pi\cdot10^{-7}\cdot\dfrac{1000^2}{0,2}\cdot50\cdot10^{-4}=0,0314H=0,0314\cdot10^3=31,4mH\)
b)Độ biến thiên từ thông:
\(\Delta\Phi=L\cdot\Delta i=0,0314\cdot\left(1-0\right)=0,0314Wb\)
Suất điện động cảm ứng:
\(e_{tc}=\left|-\dfrac{\Delta\Phi}{\Delta t}\right|=\left|-\dfrac{0,0314}{0,1}\right|=0,314V\)

Câu 9 Quan hệ giữa các loài sinh vật là:
- Quan hệ sinh vật ăn sinh vật khác
+ Trâu và cỏ Vì trâu ăn cỏ
+ Chim sáo và ve ,bét và châu chấu vì chim sáo ăn ve, bét và châu chấu
+ Châu chấu và cỏ vì châu chấu ăn cỏ
+ Chim đại bàng và chim sáo vì chim đại bàng rình rập bắt chim sáo để ăn
- Quan hệ hợp tác : Trâu và chim sáo vì chim sáo ăn ve, bét trên lưng trâu; trâu được vệ sinh và có báo động của chim khi gặp thú giữ. Quan hệ của chim sáo và trâu không phụ thuộc vào nhau chặt chẽ, không nhất thiết phải sống với nhau.
Câu 10. Trong thực tiễn sản suất, ngoài việc cung cấp đầy đủ dinh dưỡng thì người ta có các biện pháp tránh cạnh tranh gay gắt giữa các cá thể sinh vật làm giảm năng suất vật nuôi cây trồng là:
-Trong trồng trọt :
+ Trồng cây luân canh, xen canh
+ Trồng với mật độ thích hợp, chủ động tỉa thưa đúng kĩ thuật
- Trong chăn nuôi
+ Nuôi nhiều loài động vật có nhu cầu sống khác nhau trong cùng 1 môi trường sống
+ Nuôi với mật độ thích hợp, chủ động tách đàn hợp lí
Câu 11 : -Thái hóa giống là hiện tượng giống có năng suất, chất lượng giảm dần qua các thế hệ tiếp theo. Biểu hiện sinh trưởng kém, chống chịu kém, độ đồng đều thấp,…
-Một số loài tự thụ phấn hoặc thường xuyên giao phối gần lại không bị thái hóa giống vì các loài đó mang kiểu gen đồng hợp không gây hại, qua các thế hệ sẽ không xuất hiện biến dị tổ hợp gây kiểu hình thái hóa

gọi xăng là 100%
xăng tháng 10 là 1105
xăng tháng 11 là 110% : 100 x 90 = 99%
xăng tháng 11 rẻ hơn
xăng tháng 9 là 100%
xăng tháng 10 là 110%
xăng tháng 11 là 110%:100x90=99%
xăng tháng 11 ít hơn tháng trước

Bài 10: A
Bài 11:
Áp dụng hệ thức về cạnh và góc trong tam giác vào tam giác vuông, ta được:
AC = AB.tan\(^{50^0}\) = 21.tan\(^{50^0}\) \(\approx\) 25
BC = \(\dfrac{AB}{\sin C}\)= \(\dfrac{21}{sin40^0}\)\(\approx\)33
BD = \(\dfrac{AB}{\cos25^0}\)=\(\dfrac{21}{\cos25^0}\)\(\approx\)23



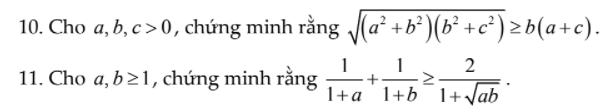 !
!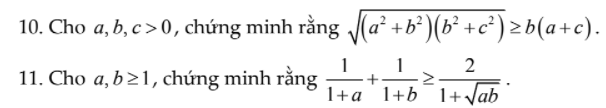
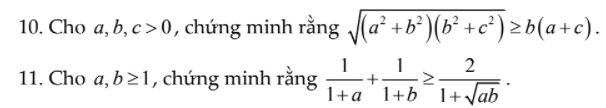
 Giải giúp mình câu 10-11
Giải giúp mình câu 10-11


10.
Do d' là ảnh của d qua phép tịnh tiến \(\Rightarrow d'\) cùng phương d
Nên pt d' có dạng: \(3x-y+c=0\) (1)
Lấy \(A\left(0;1\right)\) là 1 điểm thuộc d
Gọi \(T_{\overrightarrow{v}}\left(A\right)=A'\left(x';y'\right)\Rightarrow A'\in d'\)
Theo công thức tọa độ phép tịnh tiến:
\(\left\{{}\begin{matrix}x'=2+0=2\\y'=-3+1=-2\end{matrix}\right.\) \(\Rightarrow A'\left(2;-2\right)\)
Thế vào (1):
\(\Rightarrow3.2-\left(-2\right)+c=0\Rightarrow c=-8\)
Vậy pt d' có dạng: \(3x-y-8=0\)
11.
\(\left\{{}\begin{matrix}O\in AC\in\left(SAC\right)\\O\in BD\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow O\in\left(SAC\right)\cap\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)