Con lắc lò xo nằm ngang, độ cứng 100 N/m, có gắn vật m có khối lượng là 1 kg, được tích điện Q = 10-6 C, hệ thống được đặt trong điện trường đều nằm ngang, cường độ 2·10-6 V/m sao cho ở vi trí cân bằng lò xo bị dãn. Kéo vật để lò xo dãn 4 cm rồi truyền vận tốc \(20\sqrt{3}\) cm/s để vật dao động điều hoà. Viết phương trình dao động, chọn t = 0 lúc truyền vận tốc, trục \(Ox\uparrow\uparrow\overrightarrow{E}\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hướng dẫn:
Nhận thấy rằng, với cách kích bằng điện trường như trên sẽ làm thay đổi vị trí cân bằng của hệ mà không làm thay đổi tần số góc của hệ.
+ Tần số góc dao động của hệ ω = k m = 10 0 , 1 = 10 rad/s → T = 0,2π s.
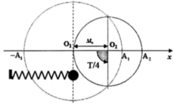
Dưới tác dụng của lực điện, con lắc sẽ dao động quanh vị trí cân bằng mới O′ cách vị trí cân bằng cũ O một đoạn O O ' = q E k = 5 cm.
+ Ta để ý rằng thời gian lực điện tồn tại đúng bằng 0,25T do vậy con lắc đi từ vị trí biên đến vị trí cân bằng mới O′, tốc độ của vật tại vị trí này là v ' = v m a x = ω A = k m Δ l 0 = 50 cm/s.
+ Ngắt điện trường, vật lại dao động quanh ví trí cân bằng cũ O, thời điểm ngắt điện trường, ta có x′ = OO′ = 5 cm.
→ Biên độ dao động mới của vật A ' = x ' 2 + v ' ω 2 = 5 2 + 50 10 2 = 5 2 cm
→ Tốc độ dao động cực đại tương ứng v ' m a x = ω A ' = 10.5 2 = 50 2 cm/s.
Đáp án B

Đáp án B
+ Lực kéo về cực đại tác dụng lên con lắc đơn F m a x = m g sin α 0 → F - m
Với giả thuyết 2 F 2 = 3 F 1 → m 2 = 1 , 5 m 1
→ m 1 + m 2 = 2 , 5 m 1 = 1 , 2 k g → m 1 = 0 , 48 k g

Tần số góc của dao động
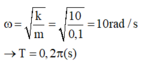
Dưới tác dụng của điện trường, con lắc dao động quanh vị trí cân bằng mới với biên độ đúng bằng độ biến dạng của lò xo tại vị trí cân bằng mới
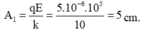
→ Ta để ý rằng, khoảng thời gian duy trì điện trường
![]()
con lắc đi đến vị trí cân bằng → Tốc độ của con lắc khi đó là
![]()
→ Ngắt điện trường, vị trí cân bằng của con lắc trở về vị trí lò xo không biến dạng → Biên độ dao động mới của con lắc lúc này là
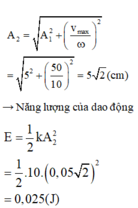
Đáp án D

Chọn đáp án B.
Độ biến dạng của lò xo tại vị trí cân bằng trong điện trường:
Δ l 0 = q E k = 10 − 6 .16.10 5 40 = 0 , 04 ( m ) = 4 ( c m ) .
→ Sau khi ngắt điện trường con lắc sẽ dao động quanh vị trí lò xo không biến dạng với biên độ:
A = Δ l 0 = 4 c m .

Chọn đáp án C
T = 2 π m k = 0 , 2 s
Vì hệ có thêm lực điện nên VTCB của vật bị dịch về phí theo chiều lò xo dãn 1 khoảng là:
Δ x = F k = E . q k = 10 5 .2.10 − 5 100 ⇒ ∆ x = 0 , 02 m = 2 c m
Suy ra tại VTCB lò xo giãn 2 cm.
Ban đầu kéo lò xo dãn 6 cm rồi thả nhẹ
→ A = 6 – 2 = 4 cm và ban đầu vật đang ở biên dương.
Vị trí lò xo không biến dạng là:
x = − 2 c m = − A 2 c m
Suy ra khoảng thời gian để vật đi qua vị trí lò xo không biến dạng lần thứ 2013 là:
Δ t = T 3 + 2013 − 1 2 . T = 201 , 3 s .

Chọn D.
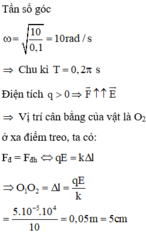

=> Vận tốc cực đại của vật sau khi ngắt điện trường:
v max = A 1 ω = 5 2 .10 = 50 2 c m




\(\omega=\sqrt{\dfrac{k}{m}}=10\left(rad\text{/}s\right)\)
\(\overrightarrow{F_đ}=Q\overrightarrow{E}\)
Vị trí cân bằng mới, lò xo đã dãn được 1 đoạn \(\Delta l=\dfrac{QE}{k}=2\left(cm\right)\)
\(t=0\left\{{}\begin{matrix}x=2cm\\v=20\sqrt{3}cm\text{/}s\end{matrix}\right.\Rightarrow A=\sqrt{x^2+\dfrac{v^2}{\omega^2}}=4\left(cm\right)\)
\(\left\{{}\begin{matrix}\cos\varphi=\dfrac{1}{2}\\\sin\varphi< 0\end{matrix}\right.\Rightarrow\varphi=-\dfrac{\pi}{3}\)
Vậy phương trình dao động của vật là: \(x=4\cos\left(10t-\dfrac{\pi}{3}\right)cm\)