Câu 17. (VD) (1,0 điểm)
Dùng thước và compa vẽ hình thoi ABCD có cạnh AB = 5 cm và đường chéo BD = 5 cm. Cắt hình thoi đó theo đường chéo nào thì nhận được hai hình tam giác đều?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
1
10 tháng 10 2023
Tham khảo:
- Vẽ đoạn thẳng AC =5 cm.
- Lấy A và C là tâm, vẽ hai đường tròn bán kính 3 cm (hình vẽ), hai đường tròn này cắt nhau tại hai điểm B và D.
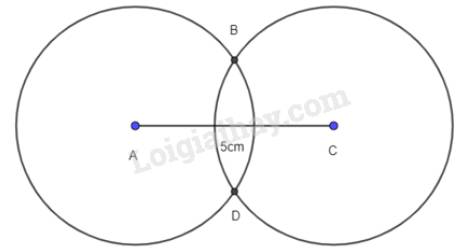
- Nối B với A, B với C, D với C.
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
Do \(ABCD\) là hình thoi nên hai đường chéo vuông góc với nhau tạo ra 4 góc vuông.
Áp dụng ĐL Pythagore vào 1 trong các tam giác vuông, ta có độ dài cạnh hình vuông là:
\(\sqrt {{{\left( {\frac{6}{2}} \right)}^2} + {{\left( {\frac{8}{2}} \right)}^2}} = \sqrt {9 + 16} = \sqrt {25} = 5\) (cm)
CM
11 tháng 6 2019
a) Hai đường chéo có vuông góc với nhau.
b) Hai đường chéo cắt nhau tại trung điểm của mỗi đường vì khi đó ta thấy :
OA=OC= 3 cm
OB= OD= 2cm.
Nhận xét: Hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
CM
28 tháng 5 2018
a) Hai đường chéo có vuông góc với nhau.
b) Hai đường chéo cắt nhau tại trung điểm của mỗi đường vì khi đó ta thấy :
OA=OC= 3 cm
OB= OD= 2cm.
Nhận xét: Hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
CM
5 tháng 11 2019
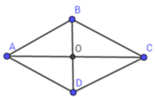
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 20 2 − 16 2 = 12
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.12.16 = 384 (cm2)
Đáp án cần chọn là: A
CM
9 tháng 5 2017
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 10 2 − 6 2 = 8
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.8.6 = 96 (cm2)
Đáp án cần chọn là: B
17 tháng 10 2021
Vì ABCD là hình thoi nên \(AB=BC=CD=DA=20\left(cm\right)\)
Và AC cắt BD tại O nên O là trung điểm AC,BD
\(\Rightarrow AC=2AO=32\left(cm\right);BD=2OB=24\left(cm\right)\)
Tham khảo: