cho tam giác abc có 2 trung tuyến bm=cn. chứng minh tam giác abc cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 9 2023
Tham khảo:
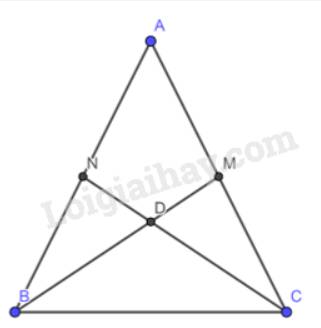
Gọi D là giao điểm của CN và BM
\( \Rightarrow \) D là trọng tâm tam giác ABC
\( \Rightarrow CD = \dfrac{2}{3}CN = BD = \dfrac{2}{3}BM\) ( do BM = CN )
\( \Rightarrow \) tam giác DBC cân tại D do BD = CD
\( \Rightarrow \) \(\widehat {DBC} = \widehat {DCB}\)(2 góc đáy trong tam giác cân) (1)
Xét \(\Delta NDB\) và \(\Delta MDC\) có :
BD = CD
\(\widehat {NDB} = \widehat {MDC}\) (2 góc đối đỉnh)
ND = DM (do cùng \( = \dfrac{1}{3}CN = \dfrac{1}{3}BM\) (tính chất của trung trực đi qua trọng tâm tam giác ))
\( \Rightarrow \Delta NDB=\Delta MDC\) (c.g.c)
\( \Rightarrow \,\widehat {NBD} = \widehat {MCD}\)(2 góc tương ứng) (2)
Từ (1) và (2) \( \Rightarrow \widehat {ABC} = \widehat {ACB}\) do \(\widehat {ABC} = \widehat {NBD} + \widehat {DBC}\) và \(\widehat {ACB} = \widehat {MCD} + \widehat {DCB}\)
\( \Rightarrow \Delta ABC\) cân tại A (do 2 góc bằng nhau)
8 tháng 3 2023
a: Xet ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
=>ΔAHB=ΔAHC
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
CB chung
=>ΔNBC=ΔMCB
=>góc GBC=góc GCB
=>ΔGCB cân tại G
c: góc ECG+góc BCG=90 độ
góc GBC+góc GEC=90 độ
mà góc BCG=góc GBC
nên góc ECG=góc GEC
=>GC=GE=GB
=>G là trung điểm của BE
Xét ΔEBC có GD//CB
nên GD/CB=EG/EB=1/2
=>CB=2GD
29 tháng 6 2023
Sửa đề: ΔABC cân tại A
AB=AC
=>1/2AB=1/2AC
=>AN=AM
Xét ΔANC và ΔAMB có
AN=AM
góc NAC chung
AC=AB
=>ΔANC=ΔAMB
=>CN=BM
22 tháng 5 2022
a: Xét ΔBNC và ΔCMB có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)
BC chung
Do đó; ΔBNC=ΔCMB
b: Sửa đề: Cm ΔANM cân tại A
Xét ΔANM có AN=AM
nên ΔANM cân tại A
NN
2
H9
HT.Phong (9A5)
CTVHS
28 tháng 3 2023
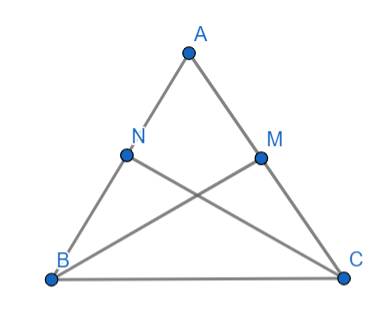
Xét △AMB và △ANC ta có:
AM=AN ( Vì M,N lần lượt là trung điểm của 2 cạnh AB, AC)
\(\widehat{A}\) là góc chung
AB=AC (Vì là hai cạnh bên trong tam giác cân)
\(\Rightarrow\Delta AMB=\Delta ANC\left(c-g-c\right)\)
\(\Rightarrow BM=CN\) (hai cạnh tương ứng)
27 tháng 3 2023
Xét ΔAMB và ΔANC có
AM=AN
góc A chug
AB=AC
=>ΔAMB=ΔANC
=>BM=CN
11 tháng 4 2023
Xét ΔABC có
BM,CN lần lượt là các đường trung tuyến
BM cắt CN tại I
=>I là trọng tâm
=>AI là đường trung tuyến của ΔACB
ΔABC cân tại A
mà AI là đường trung tuyến
nên AI vuông góc CB
=>AI là trung trực của BC
14 tháng 5 2023
Xét ΔABM và ΔACN có
AB=AC
góc BAM chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
14 tháng 5 2023
Mình xin phép sửa đề:
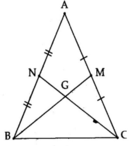
Cho tam giác ABC cân tại A , các đường trung tuyến BM và CN cắt nhau tại G
Chứng minh tam giác ABN = tam giác ACN , từ đó suy ra BM=CN
`------`
\(\text{GT | AB = AC, }\widehat{\text{B}}=\widehat{\text{C}}\)
\(\text{CM | BM = CN}\)
\(\text{BM là đường trung tuyến}\)
`->`\(\text{MA = MC (1)}\)
\(\text{CN là đường trung tuyến}\)
`->`\(\text{NA = NB (2)}\)
`\Delta ABC` cân tại A
`->`\(\widehat{\text{B}}=\widehat{\text{C}}\text{, AB = AC (3)}\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
`->`\(\text{NA = NB = MA = MC}\)
Xét `\Delta ABM` và `\Delta ACN`:
\(\left\{{}\begin{matrix}\text{BM = CN}\\\widehat{\text{B}}=\widehat{\text{C}}\\\text{BC chung}\end{matrix}\right.\)
`=> \Delta ABM = \Delta ACN (c-g-c)`
`->`\(\text{BM = CN (2 cạnh tương ứng).}\)
cái lề j thốn