tìm m để phép chia hết (x4+x3+12x2-m):(2x+5)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 12 2021
Bài 1:
a: \(=\dfrac{2x^4-8x^3+2x^2+2x^3-8x^2+2x+18x^2-72x+18+56x-15}{x^2-4x+1}\)
\(=2x^2+2x+18+\dfrac{56x-15}{x^2-4x+1}\)
29 tháng 10 2021
Bài 1:
Ta có: \(5x^3-3x^2+2x+a⋮x+1\)
\(\Leftrightarrow5x^3+5x^2-8x^2-8x+10x+10+a-10⋮x+1\)
\(\Leftrightarrow a-10=0\)
hay a=10
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
Lời giải:
a. $f(x)=x^4-3x^2+2x-7=x^3(x+2)-2x^2(x+2)+x(x+2)-7$
$=(x+2)(x^3-2x^2+x)-7=g(x)(x^3-2x^2+x)-7$
Vậy $f(x)$ chia $g(x)$ được thương là $x^3-2x^2+x$ và dư là $-7$
b. Theo phần a $f(x)=(x^3-2x^2+x)g(x)-7$
Với $x$ nguyên, để $f(x)\vdots g(x)$ thì $7\vdots g(x)$
$\Leftrightarrow x+2$ là ước của $7$
$\Rightarrow x+2\in\left\{\pm 1;\pm 7\right\}$
$\Leftrightarrow x\in\left\{-3; -1; 5; -9\right\}$
c.
Theo định lý Bezout về phép chia đa thức, để $K(x)=-2x^3+x-m\vdots x+2$ thì: $K(-2)=0$
$\Leftrightarrow -2(-2)^3+(-2)-m=0$
$\Leftrightarrow 14-m=0$
$\Leftrightarrow m=14$
CM
30 tháng 9 2018
a) Biến đổi x 2 – 2x + 1 = ( x – 1 ) 2 ; thực hiện chia được kết quả x – 1.
b) Biến đổi 8 x 3 + 27 = (2x + 3)(4 x 2 – 6x + 9); thực hiện phép chia được kết quả 4 x 2 – 6x + 9.
c) Phân thích x 6 – 6 x 4 + 12 x 2 – 8 = ( x 2 – 2)( x 4 – 4 x 2 + 4); thực hiện phép chia được kết quả - x 4 + 4 x 2 – 4.
23 tháng 2 2023
a: P(x) chia hết cho x-2
=>x^4-2x^3+3x^3-6x^2+12x^2-24x-16x+32+m-2017 chia hết cho x-2
=>m-2017=0
=>m=2017
b: P(x)=x^4+x^3+6x^2-40x+32
P(x)=0
=>x^4-2x^3+3x^3-6x^2+12x^2-24x-16x+32=0
=>(x-2)(x^3+3x^2+12x-16)=0
=>x^3+3x^2+12x-16=0 hoặc x-2=0
=>x^3-x^2+4x^2-4x+16x-16=0 hoặc x-2=0
=>x-1=0 hoặc x=2
=>x=1 hoặc x=2
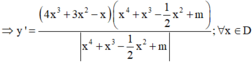
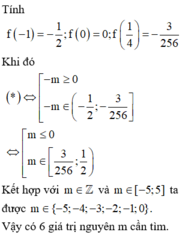
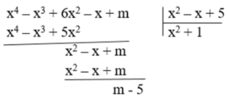
Áp dụng định lý Bơ-du ta có:
f(x) ⋮ (2x+5) ⇔ f(\(\dfrac{-5}{2}\))=0 (Kiến thức nâng cao lớp 8)
⇔ (\(\dfrac{-5}{2}\))4+(\(\dfrac{-5}{2}\))3+12.(\(\dfrac{-5}{2}\))2-m=0
⇔ \(\dfrac{1575}{16}\)-m=0
⇔ m= \(\dfrac{1575}{16}\)
Vậy m=\(\dfrac{1575}{16}\) thì x4+x3+12x2-m chia hết cho 2x+5