GIẢI PHƯƠNG TRÌNH
(X2 - x3 )/(x3 – 1) + (x2 + x + 1)/(x + 2) = 0
GIÚP MÌNH VỚI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(x – 1)(x2 + 3x – 2) – (x3 – 1) = 0
⇔ (x – 1)(x2 + 3x - 2) - (x - 1)(x2 + x + 1) = 0
⇔ (x – 1)[(x2 + 3x - 2) - (x2 + x + 1)] = 0
⇔ (x – 1). (x2 + 3x - 2 - x2 - x - 1) = 0
⇔ (x – 1)(2x - 3) = 0
⇔ x - 1 = 0 hoặc 2x - 3 = 0
+) Nếu x - 1 = 0 ⇔x = 1
+) Nếu 2x - 3 = 0 ⇔x = 3/2
Vậy tập nghiệm của phương trình là S = {1;3/2}

(x – 1)( x 2 + 5x – 2) – ( x 3 – 1) = 0
⇔ (x – 1)( x 2 + 5x – 2) – (x – 1)( x 2 + x + 1) = 0
⇔ (x – 1)[( x 2 + 5x – 2) – ( x 2 + x + 1)] = 0
⇔ (x – 1)( x 2 + 5x – 2 – x 2 – x – 1) = 0
⇔ (x – 1)(4x – 3) = 0 ⇔ x – 1 = 0 hoặc 4x – 3 = 0
x – 1 = 0 ⇔ x = 1
4x – 3 = 0 ⇔ x = 0,75
Vậy phương trình có nghiệm x = 1 hoặc x = 0,75

Ta thấy x = 1 không phải nghiệm của phương trình nên nhân 2 vế của phương trình với x - 1 ta có:
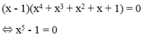
⇔ x = 1(KTM)
Vậy phương trình đã cho vô nghiệm.

Đặt x2−2x+m=tx2−2x+m=t, phương trình trở thành t2−2t+m=xt2−2t+m=x
Ta có hệ {x2−2x+m=tt2−2t+m=x{x2−2x+m=tt2−2t+m=x
⇒(x−t)(x+t−1)=0⇒(x−t)(x+t−1)=0
⇔[x=tx=1−t⇔[x=tx=1−t
⇔[x=x2−2x+mx=1−x2+2x−m⇔[x=x2−2x+mx=1−x2+2x−m
⇔[m=−x2+3xm=−x2+x+1⇔[m=−x2+3xm=−x2+x+1
Phương trình hoành độ giao điểm của y=−x2+x+1y=−x2+x+1 và y=−x2+3xy=−x2+3x:
−x2+x+1=−x2+3x−x2+x+1=−x2+3x
⇔x=12⇒y=54⇔x=12⇒y=54
Đồ thị hàm số y=−x2+3xy=−x2+3x và y=−x2+x+1y=−x2+x+1:

\(\frac{x+4}{2000}+\frac{x+3}{2001}=\frac{x+2}{2002}+\frac{x+1}{2003}\)
\(\Leftrightarrow2+\frac{x+4}{2000}+\frac{x+3}{2001}=2+\frac{x+2}{2002}+\frac{x+1}{2003}\)
\(\Leftrightarrow\left(\frac{x+4}{2000}+1\right)+\left(\frac{x+3}{2001}+1\right)=\left(\frac{x+2}{2002}+1\right)+\left(\frac{x+1}{2001}+1\right)\)
\(\Leftrightarrow\frac{x+2004}{2000}+\frac{x+2004}{2001}=\frac{x+2004}{2002}+\frac{x+2004}{2003}\)
\(\Leftrightarrow\left(x+2004\right)\left(\frac{1}{2000}+\frac{1}{2001}-\frac{1}{2002}-\frac{1}{2003}\right)=0\)
Mà \(\frac{1}{2000}+\frac{1}{2001}-\frac{1}{2002}-\frac{1}{2003}\ne0\)
Suy ra x+2004=0
\(\Leftrightarrow x=-2004\)

(x3 + x2) + (x2 + x) = 0
⇔x2 (x + 1) + x(x + 1) = 0
⇔(x2 + x)(x + 1) = 0
⇔x(x + 1)(x + 1) = 0
⇔x = 0 hoặc x + 1 = 0
⇔x = 0 hoặc x = -1
Vậy tập nghiệm của phương trình là : S = {0; -1}