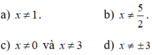x2 + (9x2)/(x+3)^2 =40
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(a,\Leftrightarrow\left(3x-1\right)\left(3x+1\right)-3\left(3x-1\right)=0\\ \Leftrightarrow\left(3x-1\right)\left(3x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\\ b,\Leftrightarrow\left(x-2\right)^2\left(x-1\right)^2-\left(x-2\right)^2-\left(x-2\right)^3=0\\ \Leftrightarrow\left(x-2\right)^2\left[\left(x-1\right)^2-1-\left(x-2\right)\right]=0\\ \Leftrightarrow\left(x-2\right)^2\left(x^2-2x+1-1-x+2\right)=0\\ \Leftrightarrow\left(x-2\right)^2\left(x^2-3x+2\right)=0\\ \Leftrightarrow\left(x-2\right)^3\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\end{matrix}\right.\)

\(1,\Leftrightarrow x^2+10x+25=x^2-4x-21\\ \Leftrightarrow14x=-46\\ \Leftrightarrow x=-\dfrac{23}{7}\\ 2,\Leftrightarrow x^3+8=15+x^3+2x\\ \Leftrightarrow2x=-7\Leftrightarrow x=-\dfrac{7}{2}\\ 3,\Leftrightarrow\left(x+3\right)^2=0\\ \Leftrightarrow x=-3\\ 4,\Leftrightarrow x^3-9x^2+27x-27=0\\ \Leftrightarrow\left(x-3\right)^3=0\\ \Leftrightarrow x-3=0\Leftrightarrow x=3\\ 5,\Leftrightarrow4x^2+4x+1-4x^2-16x-16=9\\ \Leftrightarrow-12x=24\Leftrightarrow x=-2\\ 6,\Leftrightarrow x^2-3x+5x-15=0\\ \Leftrightarrow\left(x-3\right)\left(x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)

a)
\(\left(9x^2-4\right)\left(x+1\right)=\left(3x+2\right)\left(x^2-1\right)\)
\(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)=\left(3x+2\right)\left(x+1\right)\left(x-1\right)\)
\(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[9x^2-4-\left[\left(3x+2\right)\left(x-1\right)\right]\right]=0\)
\(\Leftrightarrow\left(x+1\right)\left[9x^2-4-\left(3x^2-3x+2x-2\right)\right]=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+3x-2x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(6x^2+x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\6x^2+x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(2x-1\right)\left(3x+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{-2}{3}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{1;\dfrac{-2}{3};\dfrac{1}{2}\right\}\)
b)
\(\left(x-1\right)^2-1+x^2=\left(1-x\right)\left(x+3\right)\)
\(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
\(\Leftrightarrow x^2=1\)
\(\Leftrightarrow x=\left(\pm1\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy \(x\in\left\{1;-1\right\}\)

a) Ta có: \(A=\left(4-x\right)\left(16+4x+x^2\right)-\left(4-x\right)^3\)
\(=64-x^3+\left(x-4\right)^3\)
\(=64-x^3+x^3-12x^2+48x-64\)
\(=-12x^2+48x\)
b) Ta có: \(B=\left(3x+2\right)\left(9x^2-6x+4\right)-\left(3x-2\right)\left(9x^2+6x+4\right)\)
\(=27x^3+8-27x^3+8\)
=16
c) Ta có: \(C=\left(x+1\right)\left(x^2-x+1\right)-x\left(x+1\right)^2\)
\(=x^3+1-x\left(x^2+2x+1\right)\)
\(=x^3+1-x^3-2x^2-x\)
\(=-2x^2-x+1\)

\(a.\left(3x+2\right)\left(x^2-1\right)=\left(9x^2-4\right)\left(x+1\right)\)
\(\Leftrightarrow\left(3x+2\right)\left(x+1\right)\left(x-1\right)=\left(3x-2\right)\left(3x+2\right)\left(x+1\right)\)
\(\Leftrightarrow x-1=3x-2\)
\(\Leftrightarrow2x=1\)
\(\Leftrightarrow x=\dfrac{1}{2}\)
c: =>x-3=0
hay x=3
d: \(\Leftrightarrow\left(3x-1\right)\cdot\left(x^2+2-7x+10\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x-3\right)\left(x-4\right)=0\)
hay \(x\in\left\{\dfrac{1}{3};3;4\right\}\)

\(\left(3x+2\right)\left(x^2-1\right)=\left(9x^2-4\right)\left(x+1\right).\)
\(\Leftrightarrow\left(3x+2\right)\left(x-1\right)\left(x+1\right)-\left(3x-2\right)\left(3x+2\right)\left(x+1\right)=0.\)
\(\Leftrightarrow\left(3x+2\right)\left(x+1\right)\left(x-1-3x+2\right)=0.\)
\(\Leftrightarrow\left(3x+2\right)\left(x+1\right)\left(-2x+1\right)=0.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+2=0.\\x+1=0.\\-2x+1=0.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}.\\x=-1.\\x=\dfrac{1}{2}.\end{matrix}\right.\)
c: =>(x-3)(x2+3x+5)=0
=>x-3=0
hay x=3
d: =>(3x-1)(x2+2-7x+10)=0
=>(3x-1)(x-3)(x-4)=0
hay \(x\in\left\{\dfrac{1}{3};3;4\right\}\)

`x^2 -1-2xy+2y`
`=(x^2-1)-(2xy-2y)`
`=(x-1)(x+1)-2y(x-1)`
`=(x-1)(x+1-2y)`
__
`(x+3)^2-(2x-5)(x+3)`
`=(x+3)(x+3-2x+5)`
`=(x+3)(-x+8)`
__
`(3x+2)^2 +(3x-2)^2-2(9x^2-4)`
`= (3x+2)^2 +(3x-2)^2-2(3x-2)(3x+2)`
`= (3x+2)^2-2(3x-2)(3x+2)+(3x-2)^2`
`=[(3x+2)-(3x-2)]^2`
`=(3x+2-3x+2)^2`
`= 4^2=16`