Tính tổng:
1/2+1/4+1/8+1/16+1/32+1/64+1/128
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cộng thêm 1/2 vào biểu thức đã cho, có:
S + 1/2= 1/2+1/4+ 1/8+ 1/16+1/32+1/64+1/128
Nhận xét:
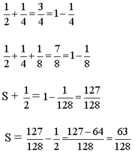


b: A=1/3+1/9+...+1/3^10
=>3A=1+1/3+...+1/3^9
=>A*2=1-1/3^10=(3^10-1)/3^10
=>A=(3^10-1)/(2*3^10)
c: C=3/2+3/8+3/32+3/128+3/512
=>4C=6+3/2+...+3/128
=>3C=6-3/512
=>C=1023/512
d: A=1/2+...+1/256
=>2A=1+1/2+...+1/128
=>A=1-1/256=255/256

a) Số các số hạng là:
( 99-49):2+1\(=\)26 ( số )
Tổng của dãy số trên là:
( 99 + 49 ) x 26 : 2 \(=\)1924
Đáp số: 1924
b) \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}+\frac{1}{8}-\frac{1}{16}+\frac{1}{16}-\frac{1}{32}+\frac{1}{32}-\frac{1}{64}+\frac{1}{64}-\frac{1}{128}\)
\(=\frac{1}{1}-\frac{1}{128}\)
\(=\frac{127}{128}\)
a) Số các số hạng là (99 - 49) : 2 + 1 = 26 số
Tổng của dãy trên là:
(99 + 49) x 26 : 2 = 1924
Đáp số : 1924
b) 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128
= 1/1 - 1/2 + 1/2 - 1/4 + 1/4 - 1/8 + 1/8 - 1/16 + 1/16 - 1/32 + 1/32 - 1/64 + 1/64 - 1/128
= 1/1 - 1/128
= 127/128

\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(=1-\frac{1}{2}+...+\frac{1}{128}=1-\frac{1}{128}=\frac{127}{128}\)

\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
đặt A = \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(A\cdot2=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\)
\(A\cdot2-A=\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\right)\) \(-\) \(\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\right)\)
\(A=\) \(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}-\frac{1}{16}-\frac{1}{32}-\frac{1}{64}-\frac{1}{128}\)
\(A=1-\frac{1}{128}\)
\(A=\frac{127}{128}\)
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
Ta lấy\(\frac{1}{128}\)là MSC. Ta tính được \(\frac{64}{128}+\frac{32}{128}+\frac{16}{128}+\frac{8}{128}+\frac{4}{128}+\frac{2}{128}+\frac{1}{128}\)
Kết quả bằng \(\frac{127}{128}\)
Đặt \(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(\Rightarrow2A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\)
\(\Rightarrow2A-A=1-\frac{1}{128}=\frac{127}{128}\)
=127/128 nhe