tìm x biết: 20x - 4x2 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
1
29 tháng 8 2023
b: 4x^2-20x+25=(x-3)^2
=>(2x-5)^2=(x-3)^2
=>(2x-5)^2-(x-3)^2=0
=>(2x-5-x+3)(2x-5+x-3)=0
=>(3x-8)(x-2)=0
=>x=8/3 hoặc x=2
c: x+x^2-x^3-x^4=0
=>x(x+1)-x^3(x+1)=0
=>(x+1)(x-x^3)=0
=>(x^3-x)(x+1)=0
=>x(x-1)(x+1)^2=0
=>\(x\in\left\{0;1;-1\right\}\)
d: 2x^3+3x^2+2x+3=0
=>x^2(2x+3)+(2x+3)=0
=>(2x+3)(x^2+1)=0
=>2x+3=0
=>x=-3/2
a: =>x^2(5x-7)-3(5x-7)=0
=>(5x-7)(x^2-3)=0
=>\(x\in\left\{\dfrac{7}{5};\sqrt{3};-\sqrt{3}\right\}\)
TM
3
TA
20 tháng 7 2021
a. `4x^2-20x+25=0`
`<=>(2x)^2-2.2x.5 +5^2=0`
`<=>(2x-5)^2=0`
`<=>2x-5=0`
`<=>x=5/2`
b. `(x-5)(x+5)-(x-3)^2=2(x-7)`
`<=>x^2-25-x^2+6x-9=2x-14`
`<=>6x-34=2x-14`
`<=>4x=20`
`<=>x=5`
20 tháng 7 2021
\(a,4x^2-20x+25=0\Leftrightarrow\left(2x\right)^2-2.2x.5+5^2=0\)
\(\Leftrightarrow\left(2x-5\right)^2=0\Leftrightarrow x=\dfrac{5}{2}\)
b, \(\left(x-5\right)\left(x+5\right)-\left(x-3\right)^2=2\left(x-7\right)\)
\(\Leftrightarrow x^2-25-x^2+6x-9=2x-14\Leftrightarrow4x=20\Leftrightarrow x=5\)
TA
29 tháng 12 2021
`(4x^2-3)^2+8=0`
`(4x^2-3)^2=-8`
Vì `(4x^2-3)^2 >=0> -8` với mọi `x` nên PT trên vô nghiệm.
23 tháng 10 2021
\(\Leftrightarrow x^2\left(x-1\right)^2-4\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)^2\left(x-2\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-2\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 7 2021
\(\Leftrightarrow x^3\left(x-2\right)+10x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x^2+10\right)=0\)
\(\Leftrightarrow x\left(x-2\right)=0\) (do \(x^2+10>0;\forall x\))
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
CM
6 tháng 7 2018
( 2 x – 3 ) 2 – 4 x 2 + 9 = 0 ⇔ ( 2 x – 3 ) 2 – ( 4 x 2 – 9 ) = 0 ⇔ ( 2 x – 3 ) 2 – ( ( 2 x ) 2 – 3 2 ) = 0 ⇔ ( 2 x – 3 ) 2 – ( 2 x – 3 ) ( 2 x + 3 ) = 0
ó (2x – 3)(2x – 3 – 2x – 3) = 0
ó (2x – 3)(-6) = 0
ó 2x – 3 = 0
ó x = 3 2
Đáp án cần chọn là: C
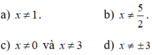
`20x - 4x^2=0`
`<=>4x(5-x)=0`
\(\Leftrightarrow\left[{}\begin{matrix}4x=0\\5-x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0:4\\x=5-0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
Vậy `x ∈ { 0; 5 }`
20x - 4x2 = 0
4x( 5 - x ) = 0
TH1: 4x = 0
x = 0 : 4
x = 0
TH2: 5 - x = 0
x = 5 - 0
x = 5
Vậy x ∈ { 0; 5 }