giúp em 3 bài này gấp vs ạ!plss
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KY
22 tháng 7 2021
1. been
2. for
3. was
4. was
5. had
6. would
7. used
8. got
9. been
10. being/swimming
11. never
12. use
TN
1
10 tháng 1 2022
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
BA
1
23 tháng 9 2021
Ta có: \(3x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{3}\Rightarrow\dfrac{x}{20}=\dfrac{y}{15}\)
\(2y=5z\Rightarrow\dfrac{y}{5}=\dfrac{z}{2}\Rightarrow\dfrac{y}{15}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{6}=\dfrac{x+z}{20+6}=\dfrac{52}{26}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=20.2=40\\y=15.2=30\\z=6.2=12\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
\(2\left(\overrightarrow{IA}+\overrightarrow{AB}\right)+3\left(\overrightarrow{IA}+\overrightarrow{AC}\right)=\overrightarrow{0}\Leftrightarrow5\overrightarrow{IA}+2\overrightarrow{AB}+3\overrightarrow{AC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AI}=\dfrac{2}{5}\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}\)
\(\overrightarrow{JB}+\overrightarrow{BA}+3\overrightarrow{JB}+3\overrightarrow{BC}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BJ}=-\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{BC}=-\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{BA}+\dfrac{3}{4}\overrightarrow{AC}\)
\(=-\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AI}.\overrightarrow{BJ}=\left(\dfrac{2}{5}\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}\right)\left(-\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\right)\)
\(=-\dfrac{2}{5}AB^2+\dfrac{9}{20}AC^2-\dfrac{3}{10}\overrightarrow{AB}.\overrightarrow{AC}\)
\(=-\dfrac{3}{5}a^2+\dfrac{9}{20}a^2-\dfrac{3}{10}a^2.cos60^0=-\dfrac{3}{10}a^2\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
b.
Từ câu a ta có
\(\overrightarrow{AI}=\dfrac{2}{5}\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}\) (1)
\(\overrightarrow{JA}+3\overrightarrow{JC}=\overrightarrow{0}\Leftrightarrow\overrightarrow{JA}+3\overrightarrow{JA}+3\overrightarrow{AC}=\overrightarrow{0}\Leftrightarrow\overrightarrow{JA}=-\dfrac{3}{4}\overrightarrow{AC}\) (2)
Cộng vế (1) và (2):
\(\overrightarrow{JA}+\overrightarrow{AI}=-\dfrac{3}{4}\overrightarrow{AC}+\dfrac{2}{5}\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}\)
\(\Leftrightarrow\overrightarrow{JI}=\dfrac{2}{5}\overrightarrow{AB}-\dfrac{3}{20}\overrightarrow{AC}\)
\(\Rightarrow IJ^2=\overrightarrow{JI}^2=\left(\dfrac{3}{5}\overrightarrow{AB}-\dfrac{3}{20}\overrightarrow{AC}\right)^2=\dfrac{9}{25}AB^2+\dfrac{9}{400}AC^2-\dfrac{9}{50}\overrightarrow{AB}.\overrightarrow{AC}\)
\(=\dfrac{9}{25}a^2+\dfrac{9}{400}a^2-\dfrac{9}{50}.a^2.cos60^0=...\)
V
0
V
0
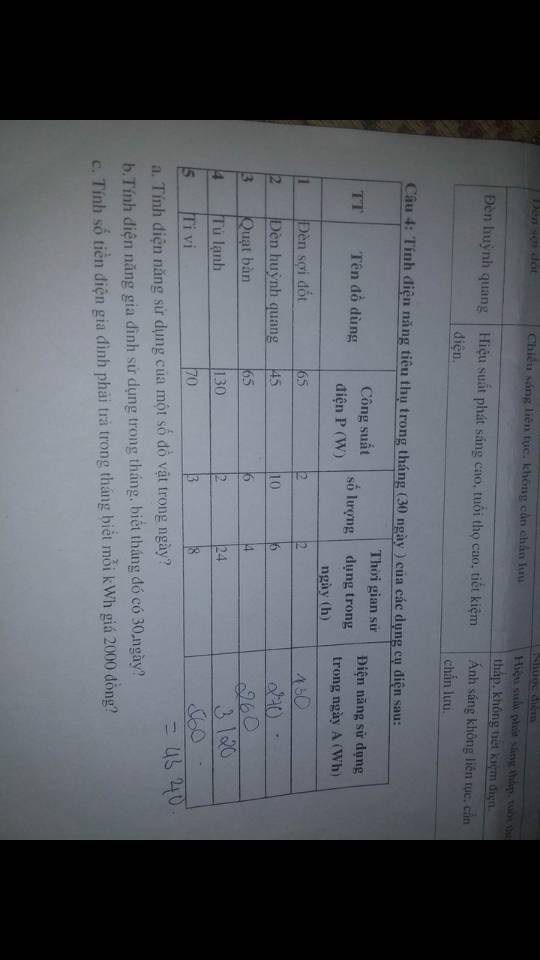
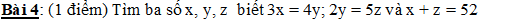
Câu 5:
\(\left\{{}\begin{matrix}x^2+y^2=4\left('\right)\\x-y-xy=2\left(''\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)^2+2xy=4\\x-y-xy=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)^2+2xy=4\left(1\right)\\2\left(x-y\right)-2xy=4\left(2\right)\end{matrix}\right.\)
Lấy \(\left(1\right)+\left(2\right)\) ta được:
\(\left(x-y\right)^2+2\left(x-y\right)=8\)
\(\Leftrightarrow\left(x-y\right)^2+2\left(x-y\right)+1-9=0\)
\(\Leftrightarrow\left(x-y+1\right)^2-9=0\)
\(\Leftrightarrow\left(x-y-2\right)\left(x-y+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-y=2\\x-y=-4\end{matrix}\right.\)
Với \(x-y=2\) Thay vào \(\left(''\right)\) ta được:
\(2-xy=2\Rightarrow xy=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-2\\y=0\Rightarrow x=2\end{matrix}\right.\)
Với \(x-y=4\Rightarrow x=4+y\) Thay vào \(\left('\right)\) ta được:
\(\left(4+y\right)^2+y^2=4\)
\(\Leftrightarrow y^2+8y+16+y^2-4=0\)
\(\Leftrightarrow2y^2+8y+12=0\)
\(\Leftrightarrow y^2+4y+6=0\)
\(\Leftrightarrow\left(y+2\right)^2+2=0\) (phương trình vô nghiệm).
Vậy hệ phương trình đã cho có nghiệm \(\left(x,y\right)\in\left\{\left(2;0\right),\left(0;-2\right)\right\}\)
Câu 6: \(\left\{{}\begin{matrix}2xy+y^2=3\left('\right)\\x^2+5xy=6\left(''\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4xy+2y^2=6\left(1\right)\\x^2+5xy=6\left(2\right)\end{matrix}\right.\)
Lấy \(\left(2\right)-\left(1\right)\) ta được:
\(x^2+xy-2y^2=0\)
\(\Leftrightarrow x^2-y^2+xy-y^2=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+y\right)+y\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+2y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=y\\x=-2y\end{matrix}\right.\)
Với \(x=y\) Thay vào \(\left('\right)\) ta được:
\(2y.y+y^2=3\)
\(\Leftrightarrow y=\pm1\Rightarrow x=\pm1\).
Với \(x=-2y\) Thay vào \(\left('\right)\) ta được:
\(2.\left(-2y\right).y+y^2=3\)
\(\Leftrightarrow y^2=-1\) (phương trình vô nghiệm)
Vậy hệ phương trình đã cho có nghiệm \(\left(x,y\right)\in\left\{\left(1;1\right),\left(-1;-1\right)\right\}\)