Ai giải giúp mk với ạ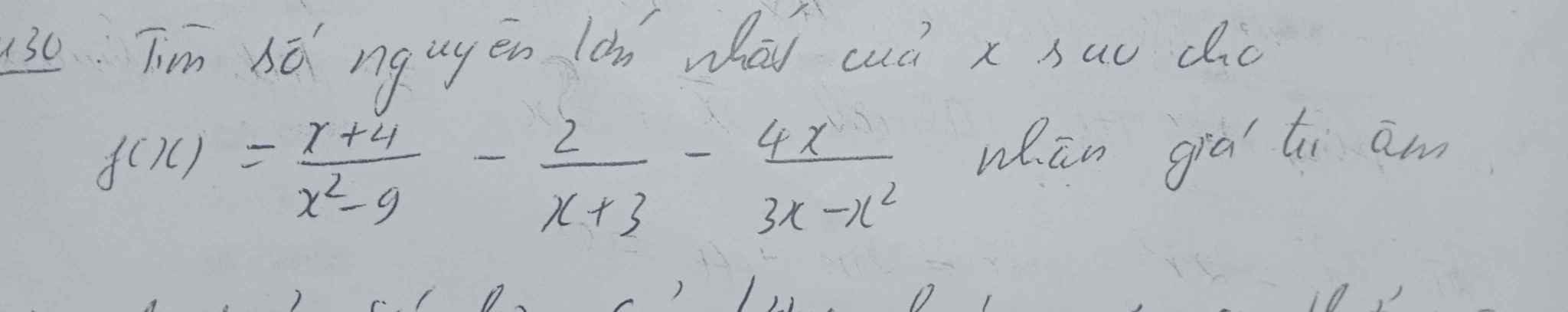
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


I.
1 D
2 B
3 D
4 A
5 C
6 A
7 A
8 C
II.
1 am listening
2 Are you playing
3 am reading/is watching
4 is cooking
5 is riding
II.
1 am listening (keep silent! . DHNB thì HTTD)
2 Are you playing ( now : DHNB thì HTTD)
3 am reading/is watching ( at the moment )
4 is cooking (at the moment DNNB thì HTTD)
5 is riding ( look)


1. Did you watch
2. have watched
3. read
4. Have you read
5. am reading
6. have finished


\(=\left(x-y\right)^2-9=\left(x-y-3\right)\left(x-y+3\right)\)
\(x^2-2xy-9+y^2=\left(x^2-2xy+y^2\right)-9=\left(x-y\right)^2-3^2=\left(x-y-3\right).\left(x-y+3\right)\)


1.
a, \(\left(C\right)x^2+y^2-6x-2y+6=0\)
\(\Leftrightarrow\left(C\right)\left(x-3\right)^2+\left(y-1\right)^2=4\)
\(\Rightarrow\) Tâm \(I=\left(3;1\right)\), bán kính \(R=2\)
b, Tiếp tuyến đi qua A có dạng: \(\left(\Delta\right)ax+by-5a-7b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I;\Delta\right)=\dfrac{\left|3a+b-5a-7b\right|}{\sqrt{a^2+b^2}}=2\)
\(\Leftrightarrow\left|a+3b\right|=\sqrt{a^2+b^2}\)
\(\Leftrightarrow6ab+8b^2=0\)
\(\Leftrightarrow2b\left(3a+4b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}b=0\\3a+4b=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\Delta_1:x=5\\\Delta_2:4x-3y+1=0\end{matrix}\right.\)
TH1: \(\Delta_1:x=5\)
Tiếp điểm có tọa độ là nghiệm hệ: \(\left\{{}\begin{matrix}x=5\\x^2+y^2-6x-2y+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y^2-2y+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\Rightarrow\left(5;1\right)\)
TH2: \(\Delta_2:4x-3y+1=0\)
Tiếp điểm có tọa độ là nghiệm hệ: \(\left\{{}\begin{matrix}4x-3y+1=0\\x^2+y^2-6x-2y+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7}{5}\\y=\dfrac{11}{5}\end{matrix}\right.\Rightarrow\left(\dfrac{7}{5};\dfrac{11}{5}\right)\)
Kết luận: Phương trình tiếp tuyến: \(\left\{{}\begin{matrix}\Delta_1:x=5\\\Delta_2:4x-3y+1=0\end{matrix}\right.\)
Tọa độ tiếp điểm: \(\left\{{}\begin{matrix}\left(5;1\right)\\\left(\dfrac{7}{5};\dfrac{11}{5}\right)\end{matrix}\right.\)


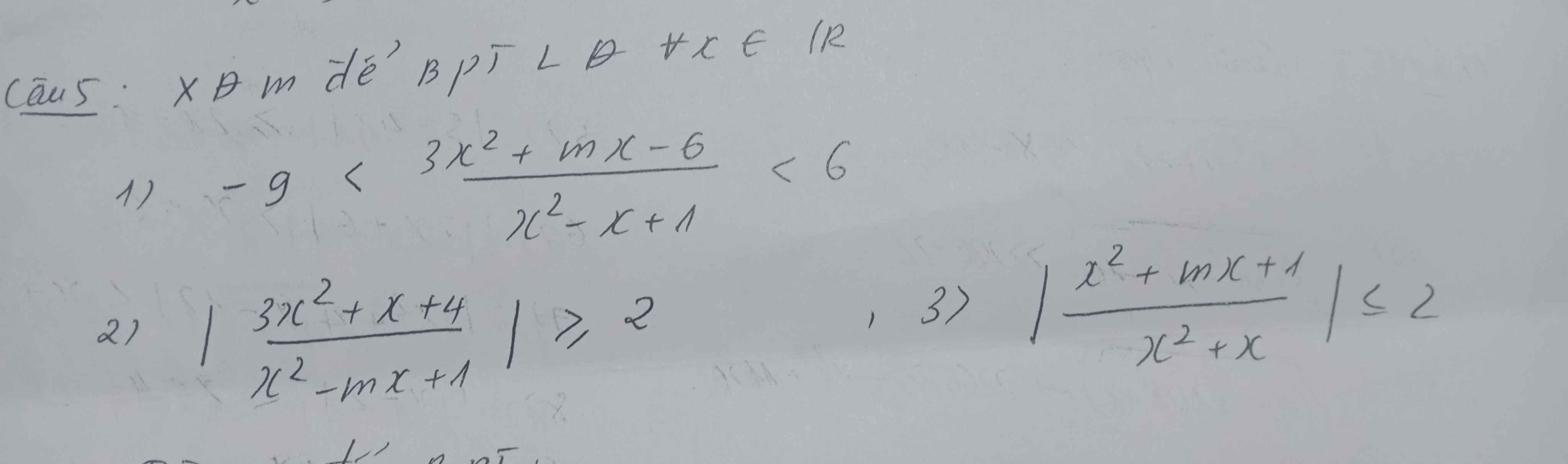





\(f\left(x\right)=\dfrac{x+4}{\left(x-3\right)\left(x+3\right)}-\dfrac{2}{x+3}+\dfrac{4x}{x\left(x-3\right)}\)
\(f\left(x\right)=\dfrac{x\left(x+4\right)}{x\left(x-3\right)\left(x+3\right)}-\dfrac{2x\left(x-3\right)}{x\left(x+3\right)\left(x-3\right)}+\dfrac{4x\left(x+3\right)}{x\left(x-3\right)\left(x+3\right)}\)
\(f\left(x\right)=\dfrac{3x^2+22x}{x\left(x-3\right)\left(x+3\right)}\)
\(f\left(x\right)< 0\Leftrightarrow\left\{{}\begin{matrix}x< -\dfrac{22}{3}\\-3< x< 0\\0< x< 3\end{matrix}\right.\) \(\Rightarrow x_{max}=2\)