1.Tìm hệ số của x4 trong khai triển (1+x)6
2. Một hộp đựng 20 quả cầu trong đó có 15 quả cầu xanh và 5 quả cầu đỏ, chọn ngẫu nhiên hai quả cầu từ hộp. Tính xác suất để chọn được hai quả khác màu.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số cách chọn hai quả cầu cùng màu là:
\(5\cdot4+3\cdot2=26\left(cách\right)\)
Số quả cầu tất cả là 5+3=8(quả)
Xác suất để chọn hai quả cầu cùng màu là:
\(\dfrac{26}{8\cdot7}=\dfrac{13}{28}\)

Không gian mẫu: \(C_{15}^3=455\)
Số cách chọn 3 quả sao cho vừa khác màu vừa khác số:
\(4.4.4=64\)
Xác suất: \(P=\dfrac{64}{455}\)

Chọn D
Gọi Ω là không gian mẫu, ta có n( Ω ) = C 15 6 = 5005.
Gọi A là biến cố: “6 quả lấy được có đủ ba màu”
A ¯ : “6 quả lấy được không có đủ ba màu”.
TH1: 6 quả lấy được chỉ một màu đỏ có C 6 6 = 1cách.
TH2: 6 quả lấy được có hai màu
+ 6 quả lấy được có hai màu đỏ và xanh: có ![]() cách.
cách.
+ 6 quả lấy được có hai màu đỏ và vàng: có ![]() cách.
cách.
+ 6 quả lấy được có hai màu đỏ và xanh: có ![]() cách.
cách.
![]()
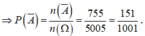
Vậy 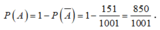

Đáp án C
Số cách để chọn 2 quả cầu từ hộp là ![]()
Tiếp theo ta sẽ tìm số cách để lấy 2 quả cầu cùng màu từ hộp
Trường hợp 1: Chọn được hai quả cầu màu xanh => có ![]() cách chọn
cách chọn
Trường hợp 2: Chọn được hai quả cầu màu đỏ=> có ![]() cách chọn
cách chọn
Do đó số cách được chọn 2 quả cầu cùng màu là 

Đáp án C
Chọn ngẫu nhiên hai quả cầu: C 11 2
Hai quả cầu chọn ra cùng màu: C 5 2 + C 6 2
Vậy xác suất để chọn ra hai quả cầu cùng màu là
![]()

Đáp án C
Chọn ngẫu nhiên hai quả cầu: C 11 2
Hai quả cầu chọn ra cùng màu: C 5 2 + C 6 2
Vậy xác suất để chọn ra hai quả cầu cùng màu là:
p = C 5 2 + C 6 2 C 11 2 = 5 11
1) \(\left(1+x\right)^6=\sum\limits^6_{k=0}C^k_6x^k\)
Số hạng chứa \(x^4\) có \(k=4\)
Hệ số của \(x^4\) trong khai triển là: \(C_6^4=15\).
2)
\(n\left(\Omega\right)=C_{20}^2=190\)
A: "Hai quả được chọn khác màu"
\(\overline{A}\): "Hai quả được chọn cùng màu".
\(n\left(\overline{A}\right)=C_{15}^2+C_5^2=115\)
\(n\left(A\right)=190-115=75\)
\(P\left(A\right)=\dfrac{75}{190}=\dfrac{15}{38}\)