Giải giúp với ạ. (Cần gấp ạ) 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
83
2
S
16 tháng 1 2022
PTHH : 2Al + 6HCl --> 2AlCl3 + 3H2 ↑ (1)
nAlCl3 = \(\dfrac{m}{M}=\dfrac{13,35}{27+35,5.3}=0.1\left(mol\right)\)
Từ (1) => nHCl = 2nH2 = 0.2 (mol)
=> mHCl = n.M = 0.2 x 36.5 = 7.3 (g)
16 tháng 1 2022
\(PTHH:2Al+6HCl\rightarrow2AlCl_3+3H_2\\ n_{AlCl_3}=\dfrac{m}{M}=\dfrac{13,35}{133,5}=0,1\left(mol\right)\\ Theo.PTHH:n_{HCl}=3.n_{AlCl_3}=3.0,1=0,3\left(mol\right)\\ m_{HCl}=n.M=0,3.36,5=10,95\left(g\right)\)
TH
3
27 tháng 7 2023
\(...=\dfrac{152}{10}-\dfrac{15}{9}+\dfrac{48}{10}-\dfrac{4}{19}=\dfrac{76}{5}-\dfrac{5}{3}+\dfrac{24}{5}-\dfrac{4}{19}\)
\(=\dfrac{76}{5}-\dfrac{5}{3}+\dfrac{24}{5}-\dfrac{4}{19}=\dfrac{76}{5}+\dfrac{24}{5}-\dfrac{5}{3}-\dfrac{4}{19}\)
\(=\dfrac{100}{5}-\dfrac{5}{3}-\dfrac{4}{19}=20-\dfrac{5}{3}-\dfrac{4}{19}=\dfrac{20.57-5.19-4.3}{57}=\dfrac{1033}{57}\)
NT
3
6 tháng 5 2021
a. Đoạn trích trên trích từ văn bản "Sống chết mặc bay" của tác giả Phạm Duy Tốn.
b. BPTT: Liệt kê, điệp ngữ. Tác dụng: tác giả đã sử dụng biện pháp liệt kê và điệp ngữ nhằm tạo nhịp điệu, tăng sức biểu đạt, tăng sức gợi hình gợi cảm cho bài văn thêm sinh động.
TM
0
HP
8 tháng 5 2021
1.
Cơ năng ban đầu: \(W=W_đ+W_t=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}.4.2^2+4.10.5=208\left(J\right)\)
Cơ năng tại độ cao cực đại:
\(W_{\left(1\right)}=W_{đ\left(1\right)}+W_{t\left(1\right)}\)
\(=\dfrac{1}{2}mv_{\left(1\right)}^2+mgz_{\left(1\right)}\)
\(=mgh_{max}\)
\(=40h_{max}\)
Định luật bảo toàn cơ năng:
\(W=W_{\left(1\right)}\)
\(\Leftrightarrow208=40h_{max}\)
\(\Rightarrow h_{max}=5,2\left(m\right)\)
Vậy độ cao cực đại là \(h_{max}=5,2m\)
DT
2
AH
Akai Haruma
Giáo viên
18 tháng 11 2021
Lời giải:
a. ĐKXĐ: $x>0; x\neq 4$
b.
\(M=\sqrt{x}.\left[\frac{1}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}\right].\frac{x-4}{2\sqrt{x}}\)
\(=\frac{2\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{x-4}{2}=\frac{2\sqrt{x}}{x-4}.\frac{x-4}{2}=\sqrt{x}\)
c. Để $M>3\Leftrightarrow \sqrt{x}>3\Leftrightarrow x>9$
Kết hợp đkxđ suy ra $x>9$ thì $M>3$
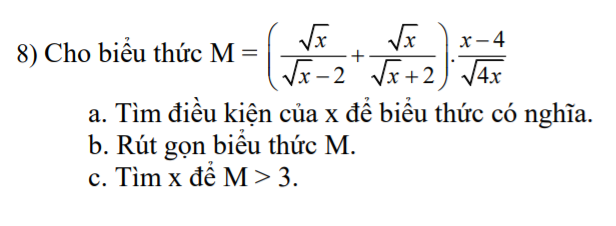
thể tích của vật đó là
`V=m/D =5,2/2600=2*10^(-3) m^3`
Do vật đc nhúng chìm hoàn toàn
nên lực đẩy Ác si mét t/d lên vật là
`F_A= d_n *V=2*10^(-3) *10000=20(N)`