Cho tam giác ABC vuông tại A. Gọi D là trung điểm của cạnh BC. Kẻ DE vuông góc AB, DF vuông góc AC
a) Chứng minh DA = DF
b) Chứng minh tứ giác AHEF là hình bình hành và tứ giác AHBD là hình thoi
c) Trên tia đối của tia FD lấy I sao cho FI = FD. Chứng minh I đối xứng với H qua A


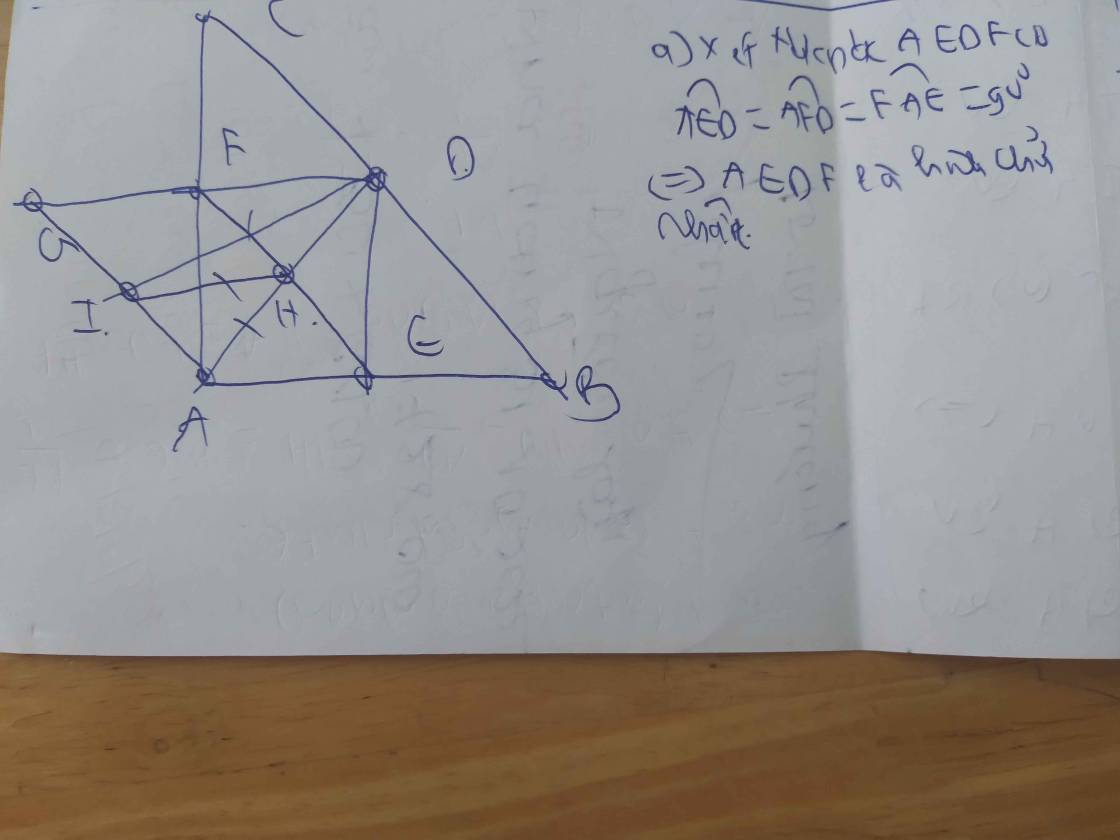



a: Sửa đề; DA=EF
Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
nen AEDF là hình chữ nhật
=>DA=EF
b: Xét tứ giác AFEH có
AF//HE
AF=HE
Do đó: AFEH là hình bình hành
XétΔABC có
Dlà trung điểm của BC
DE//AC
Do đó E là trung điểm của AB
Xét ΔABC có
D là trung điểm của BC
DF//AB
Do đó:F là trung điểm của AC
Xét tứ giác AHBD có
E là trung điểm chung của AB và HD
AB vuông góc với HD
Do đó: AHBD là hình thoi
=>AB là phân giác của góc HAD(1)
c: Xét tứ giác ADCI có
F là trung điểm chung của AC và DI
DA=DC
Do đó: ADCI là hình thoi
=>AC là phân giác của góc DAI(2)
Từ (1), (2) suy ra góc IAH=2*90=180 độ
=>I,A,H thẳng hàng
mà AI=AH
nên A là trung điểm của IH