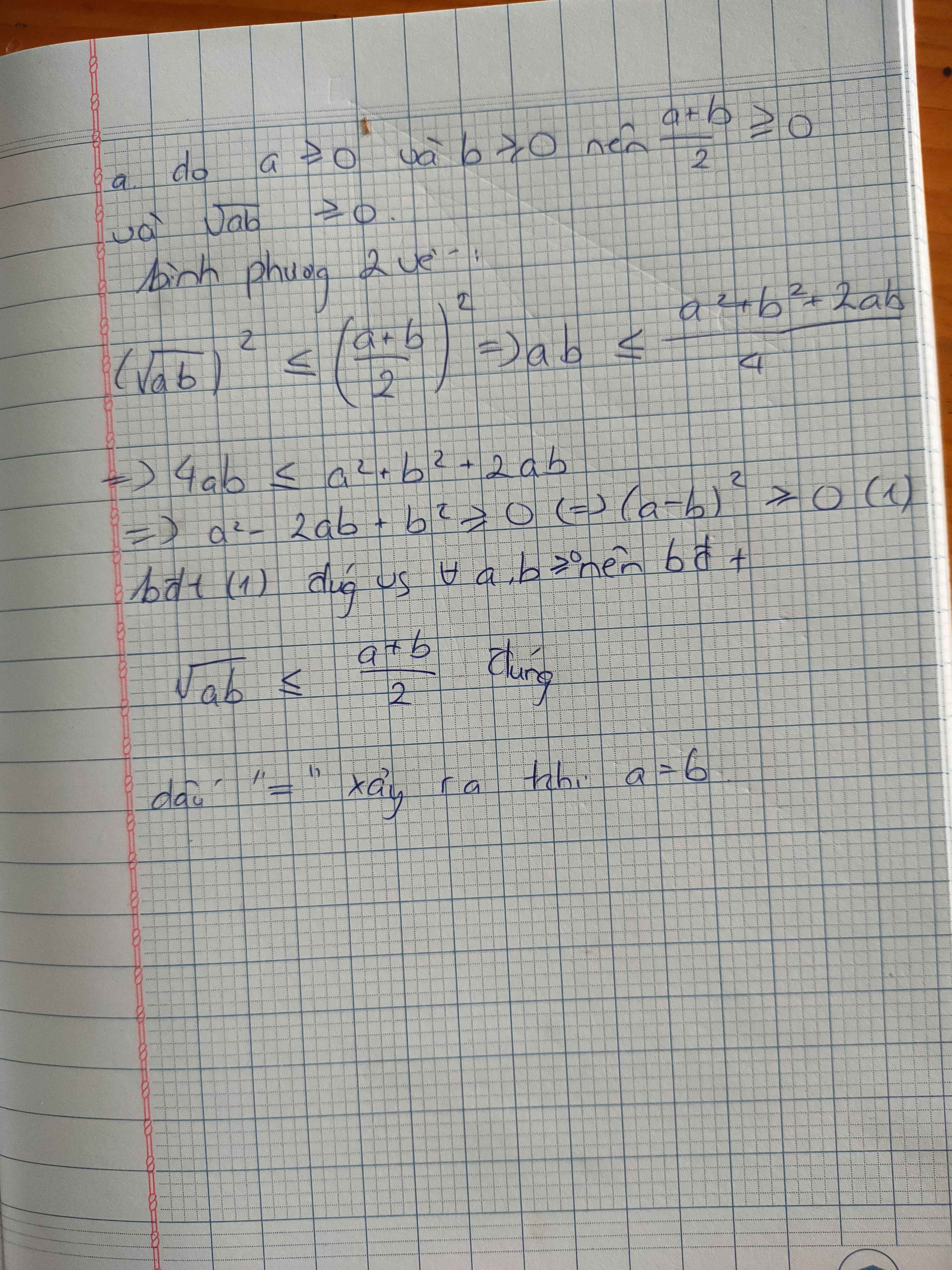Chứng minh 0<A<1 với A=\(\frac{1}{2}+\frac{1}{^22}+\frac{1}{^32}+....+\frac{1}{^{100}2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 5 2018
a) Chú ý m > 2 thì m > 0.
b) Chú ý a < 0 và b < 0 thì ab > 0. Khi đó a > b, nhân hai vế với 1 ab > 0 ta thu được 1 b > 1 a . Tương tự a > 0, b > 0, a > b ta được 1 a < 1 b .
CM
25 tháng 4 2017
a) Ta có M < 1. Mà m > 0 nên m.m < m.1 hay m 2 < m.
b) Từ a > b > 0, ta suy ra được a 2 > ab > b 2 . Sử dụng tính chất bắc cầu và liên hệ giữa thứ tự với phép cộng ta có a 2 - b 2 > 0.
KA
1
28 tháng 6 2021
`sqrta+1>sqrt{a+1}`
`<=>a+2sqrta+1>a+1`
`<=>2sqrta>0`
`<=>sqrta>0AAa>0`
`sqrt{a-1}<sqrta`
`<=>a-1<a`
`<=>-1<0` luôn đúng
`sqrt6-1>sqrt3-sqrt2`
`<=>sqrt6-sqrt3+sqrt2-1>0`
`<=>sqrt3(sqrt2-1)+sqrt2-1>0`
`<=>(sqrt2-1)(sqrt3+1)>0` luôn đúng
R
18 tháng 2 2022
\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}\)
1 tháng 4 2023
a: \(\dfrac{a}{b}+\dfrac{b}{a}>=2\cdot\sqrt{\dfrac{a}{b}\cdot\dfrac{b}{a}}=2\)
b: a<b
=>-2a>-2b
=>-2a-3>-2b-3
c: =x^2+2xy+y^2+y^2+6y+9
=(x+y)^2+(y+3)^2>=0 với mọi x,y
d: a+3>b+3
=>a>b
=>-5a<-5b
=>-5a+1<-5b+1
29 tháng 11 2021
\(4,VT=-a+b+c-a+b-c+a-b-c=-a+b-c=-\left(a-b+c\right)=VP\\ 5,M=-a+b-b-c+a+c-a=-a\\ M>0\Rightarrow-a>0\Rightarrow a< 0\)
11 tháng 3 2017
a vì a+2>5 =>a+2+(-2)>5+(-2)=>a+2>3
b vì a>3 => a+2>3+2 =>a+2>5
c vì m>n =>m-n>n-n=>m-n>0
đ vì m-n=0 =>m-n+n>0+n=>m>n
e vì m<n nên m+(-4)<n+(-4) =>m-4<n-4 (1)
vì -4>-5 => m-4>m-5 (2)
từ (1) và (2) =>m-5<n-4
13 tháng 4 2017
2) \(x^4-x^2+1=0\)(1)
Đặt: t=x2, khi đó:
(1)\(\Leftrightarrow t^2-t+1=0\)
\(\Leftrightarrow\left(t-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\left(2\right)\)
\(\Rightarrow\left(2\right)\) vô nghiệm => (1) vô nghiệm
PT
1
CM
23 tháng 5 2019
Vì a ≥ 0 nên a xác định, b ≥ 0 nên b xác định
Ta có: a - b 2 ≥ 0 ⇒ a - 2 a b + b ≥ 0 ⇒ a + b ≥ 2 a b
⇒ a + b + a + b ≥ a + b + 2 a b
⇒ 2(a + b) ≥ a 2 + 2 a b + b 2
15 tháng 2 2016
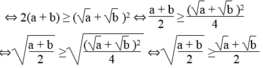
ôi dào !dễ ợt ! cô em mới cho học ngày hôm qua !k đi rùi em trình bày cho cách làm !