Câu 3. Cho tam giác $A B C$ thoả mãn $\dfrac{a^3+b^3-c^3}{a+b-c}=c^2$. Chứng minh $\widehat{C}=60^{\circ}$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 9 2023
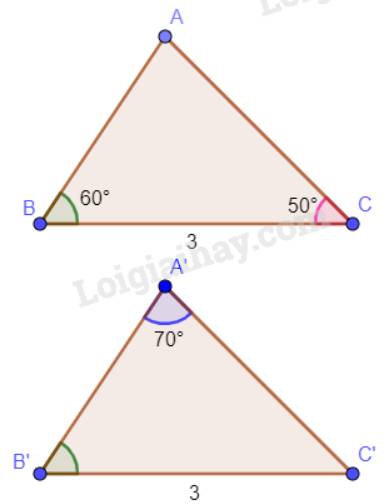
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 12 2020
\(VT=\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}=\dfrac{a^2}{ab+ac}+\dfrac{b^2}{bc+ab}+\dfrac{c^2}{ac+bc}\)
\(VT\ge\dfrac{\left(a+b+c\right)^2}{2\left(ab+bc+ca\right)}\ge\dfrac{3\left(ab+bc+ca\right)}{2\left(ab+bc+ca\right)}=\dfrac{3}{2}\)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c\)
\(\Rightarrow\) Tam giác là tam giác đều
17 tháng 5 2022
Bài này xuất hiện trong câu cuối đề GKI năm ngoái của mình :v
-Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\left\{{}\begin{matrix}\dfrac{a}{2020}=\dfrac{c}{2022}=\dfrac{a-c}{2020-2022}=\dfrac{a-c}{-2}\\\dfrac{a}{2020}=\dfrac{b}{2021}=\dfrac{a-b}{2020-2021}=\dfrac{a-b}{-1}\\\dfrac{c}{2022}=\dfrac{b}{2021}=\dfrac{c-b}{2022-2021}=c-b\end{matrix}\right.\)
\(\Rightarrow c-b=-\left(a-b\right)=\dfrac{a-c}{-2}\)
\(\Rightarrow\left\{{}\begin{matrix}a-c=-2\left(c-b\right)\\a-b=-\left(c-b\right)\end{matrix}\right.\)
\(\left(a-c\right)^3+8\left(a-b\right)^2.\left(c-b\right)=\left[-2\left(c-b\right)\right]^3+8\left[-\left(c-b\right)\right]^2.\left(c-b\right)=-8\left(c-b\right)^3+8\left(c-b\right)^3=0\left(đpcm\right)\)
25 tháng 6 2023
Áp dụng bất đẳng thức Cô si cho hai số dương ta có:
(a2 + b2) + (b2 + c2) + (c2 + a2) ≥ 2ab + 2bc + 2ca
=> 2(a2 + b2 + c2 ) ≥ 2 (ab + bc + ca) (1) (a2 + 1) + (b2 + c2) + (c2 + a2) ≥ 2a + 2b + 2c
=> a2 + b2 + c2 + 3 ≥ 2(a + b + c) (2)
Cộng các vế của (1) và (2) ta có:
3 ( a2 + b2 + c2 ) + 3 ≥ 2 (ab + bc + ca + a + b + c)
=> 3( a2 + b2 + c2 ) + 3 ≥ 12 => a2 + b2 + c2 ≥ 3.
Ta có: (a^3/b + ab ) + ( b^3/c + bc ) + ( c^3/a + ca)≥ 2(a2 + b2 + c2) (CÔ SI)
<=>a^3/b + b^3/c + c^3/a +ab + bc + ac ≥ 2(a2 + b2 + c2)
Vì a2 + b2 + c2 ≥ ab + bc + ca => a^3 + b^3 + c^3 ≥ a2 + b2 + c2 ≥ 3 (đpcm).
TA
25 tháng 6 2023
Áp dụng bất đẳng thức cô-si cho hai số dương ta có:
\(\left(a^2+b^2\right)+\left(b^2+c^2\right)+\left(c^2+a^2\right)\ge2ab+2bc+2ca\)
\(\Rightarrow2\left(a^2+b^2+c^2\right)\ge2\left(ab+bc+ca\right)\) (1)
\(\left(a^2+b^2\right)+\left(b^2+c^2\right)+\left(c^2+a^2\right)\ge2a+2b+2c\)
\(\Rightarrow a^2+b^2+c^2+3\ge2\left(a+b+c\right)\) (2)
Cộng (1) với (2)
\(3\left(a^2+b^2+c^2\right)+3\ge2\left(ab+bc+ca+a+b+c\right)\)
\(\Rightarrow3\left(a^2+b^2+c^2\right)+3\ge12\)
\(\Rightarrow a^2+b^2+c^2\ge3\)
Ta có: \(\left(\dfrac{a^3}{b}+ab\right)+\left(\dfrac{b^3}{c}+bc\right)+\left(\dfrac{c^3}{a}+ca\right)\ge2\left(a^2+b^2+c^2\right)\)
\(\Leftrightarrow\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}+ab+bc+ca\ge2\left(a^2+b^2+c^2\right)\)
Vì \(a^2+b^2+c^2\ge ab+bc+ca\)
\(\Rightarrow\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}\ge a^2+b^2+c^2\ge3\) (đpcm).
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 8 2021
\(3=ab+bc+ca\ge3\sqrt[3]{\left(abc\right)^2}\Rightarrow abc\le1\)
\(\dfrac{1}{1+a^2\left(b+c\right)}=\dfrac{1}{1+a\left(ab+ac\right)}=\dfrac{1}{1+a\left(3-bc\right)}=\dfrac{1}{1+3a-abc}=\dfrac{1}{3a+\left(1-abc\right)}\le\dfrac{1}{3a}\)
Tương tự và cộng lại:
\(VT\le\dfrac{1}{3a}+\dfrac{1}{3b}+\dfrac{1}{3c}=\dfrac{ab+bc+ca}{3abc}=\dfrac{3}{3abc}=\dfrac{1}{abc}\)
15 tháng 9 2023
a) Từ giả thiết : \(\dfrac{1}{a}+\dfrac{1}{b}\text{=}\dfrac{1}{c}\)
\(\Rightarrow2ab\text{=}2bc+2ca\)
\(\Rightarrow2ab-2bc-2ca\text{=}0\)
Ta xét : \(\left(a+b-c\right)^2\text{=}a^2+b^2+c^2+2ab-2bc-2ca\)
\(\text{=}a^2+b^2+c^2\)
Do đó : \(A\text{=}\sqrt{a^2+b^2+c^2}\text{=}\sqrt{\left(a+b-c\right)^2}\)
\(\Rightarrow A\text{=}a+b-c\)
Vì a;b;c là các số hữu tỉ suy ra : đpcm
b) Đặt : \(a\text{=}\dfrac{1}{x-y};b\text{=}\dfrac{1}{y-x};c\text{=}\dfrac{1}{z-x}\)
Do đó : \(\dfrac{1}{a}+\dfrac{1}{b}\text{=}\dfrac{1}{c}\)
Ta có : \(B\text{=}\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}\)
Từ đây ta thấy giống phần a nên :
\(B\text{=}a+b-c\)
\(B\text{=}\dfrac{1}{x-y}+\dfrac{1}{y-z}-\dfrac{1}{z-x}\)
Suy ra : đpcm.
Mình bổ sung đề phần b cần phải có điều kiện của x;y;z nha bạn.
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
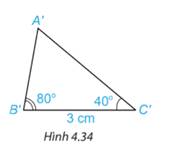
A’B’=2,2 cm
A’C’=3,4 cm
Hai tam giác \(ABC\) và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau.
huyh
Do a, b, c là độ dài 3 cạnh của tam giác ABC nên \(a+b-c\ne0\). Như vậy, \(\dfrac{a^3+b^3-c^3}{a+b-c}=c^2\)
\(\Leftrightarrow a^3+b^3-c^3=c^2a+c^2b-c^3\)
\(\Leftrightarrow a^3+b^3-c^2a-c^2b=0\)
\(\Leftrightarrow\left(a+b\right)\left(a^2-ab+b^2\right)-c^2\left(a+b\right)=0\)
\(\Leftrightarrow\left(a+b\right)\left(a^2-ab+b^2-c^2\right)=0\)
\(\Leftrightarrow a^2-ab+b^2-c^2=0\) (do \(a+b\ne0\))
\(\Leftrightarrow c^2=a^2+b^2-ab\) (1)
Mặt khác, theo định lý cosin, ta có \(c^2=a^2+b^2-2ab.\cos C\) (2)
Từ (1) và (2), ta thu được \(2\cos C=1\Leftrightarrow\cos C=\dfrac{1}{2}\Leftrightarrow\widehat{C}=60^o\)
Vậy \(\widehat{C}=60^o\)