Cho (O) đường kính AB. Lấy C thuộc (O), gọi E là trung điểm BC. Tiếp tuyến tại C của (O) cắt OE ở D.
a) Chứng minh: AACB vuông và OE vuông góc BC.
b) Chứng minh: DB là tiếp tuyến của (O).
c) Kẻ CH vuông góc AB. Chứng minh: CB.OC=OD.HC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét (O) có
ΔBAC nội tiếp đường tròn
AB là đường kính
Do đó: ΔBAC vuông tại C
Xét (O) có
OE là một phần đường kính
BC là dây
E là trung điểm của BC
Do đó: OE\(\perp\)BC
c: Xét ΔDEC vuông tại E và ΔDEB vuông tại E có
DE chung
CE=BE
Do đó: ΔDEC=ΔDEB
Suy ra: DC=DB
Xét ΔOBD và ΔOCD có
OB=OC
OD chung
DB=DC
Do đó: ΔOBD=ΔOCD
Suy ra: \(\widehat{OBD}=\widehat{OCD}\)
\(\Leftrightarrow\widehat{OBD}=90^0\)
hay DB là tiếp tuyến có B là tiếp điểm của (O)

b: Xét (O) có
ΔBAC nội tiếp đường tròn
AB là đường kính
Do đó: ΔBAC vuông tại C
Xét (O) có
OE là một phần đường kính
BC là dây
E là trung điểm của BC
Do đó: OE\(\perp\)BC tại E
c: Xét ΔDEC vuông tại E và ΔDEB vuông tại E có
DE chung
CE=BE
Do đó: ΔDEC=ΔDEB
Suy ra: DC=DB
Xét ΔOCD và ΔOBD có
OC=OB
DC=DB
OD chung
Do đó: ΔOCD=ΔOBD
Suy ra: \(\widehat{OCD}=\widehat{OBD}\)
\(\Leftrightarrow\widehat{OCD}=90^0\)
hay DB là tiếp tuyến của (O)

b: Xét (O) có
ΔABC nội tiếp đường tròn
AB là đường kính
Do đó: ΔABC vuông tại C
Xét ΔABC có
O là trung điểm của AB
E là trung điểm của BC
Do đó: OE là đường trung bình của ΔBAC
Suy ra: OE\(\perp\)CB
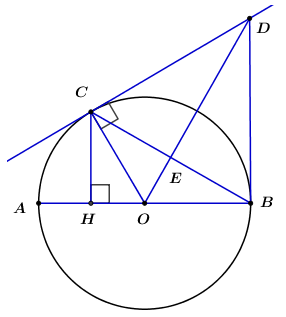
a) Xét đường tròn (O) có AB là đường kính và △ ABC nội tiếp đường tròn (O)
⇒ \(\widehat{ACB}=90^0\) hay △ ABC vuông tại C.
Có: OC = OB (do cùng bằng bán kính), suy ra O cách đều hai điểm C và B,
⇒ O nằm trên trung trực của BC.
Có EC = EB (do E là trung điểm của BC), suy ra E cách đều hai điểm B và C
⇒ E nằm trên trung trực của BC.
Ta có E và O đều nằm trên đường trung trực của đoạn BC
⇒ OE là trung trực của đoạn BC.
⇒ OE ⊥ BC (đpcm)
b) Vì tiếp tuyến tại C của (O) cắt OE ở D nên ta có D nằm trên EO, suy ra D nằm trên đường trung trực của BC ⇒ DB = DC (tính chất đường trung trực)
Xét ΔCOD và ΔBOD có:
OC = OB (do cùng là bán kính của đường tròn)
OD chung
DB = DC (cmt)
⇒ ΔCOD = ΔBOD ( c − c − c )
⇒ \(\widehat{OCD}=\widehat{OBD}=90^0\)
⇒ BD ⊥ OB
Suy ra DB là tiếp tuyến của (O) (đpcm).
c)Vì DB là tiếp tuyến của (O) (cmt)
⇒ \(\widehat{OBD}=90^0\) ⇒ \(\widehat{CBO}+\widehat{CBD}=90^0\) \(\left(1\right)\)
Vì OD là trung trực của BC (cmt)
⇒ OD ⊥ BC ⇒ \(\widehat{DEB}=90^0\)⇒ \(\widehat{ODB}+\widehat{CBD}=90^0\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ⇒ \(\widehat{CBO}=\widehat{ODB}\) ( cùng phụ với \(\widehat{DBC}\) )
Xét △ ODB và △ CBH có:
\(\widehat{CHB}=\widehat{OBD}=90^0\)
\(\widehat{CBO}=\widehat{ODB}\) ( cmt )
⇒ △ ODB \(\approx\) △ CBH ( g − g )
⇒ \(\dfrac{OB}{CH}=\dfrac{OD}{BC}\)
⇒ OB . BC = OD . CH
⇒ △ ODB ∼ △ CBH ( g − g )
Mà có OB = OC (do cùng là bán kính của đường tròn)
Suy ra: CB.OC=OD.HC (đpcm)

b: Xét (O) có
ΔABC nội tiếp đường tròn
AB là đường kính
Do đó: ΔABC vuông tại C
Xét (O) có
OE là một phần đường kính
CB là dây
E là trung điểm của CB
Do đó: OE\(\perp\)BC
c: Xét ΔDEC vuông tại E và ΔDEB vuông tại E có
DE chung
EC=EB
Do đó: ΔDEC=ΔDEB
Suy ra: DC=DB
Xét ΔOCD và ΔOBD có
OC=OB
OD chung
CD=BD
Do đó: ΔOCD=ΔOBD
Suy ra: \(\widehat{OCD}=\widehat{OBD}\)
mà \(\widehat{OCD}=90^0\)
nên \(\widehat{OBD}=90^0\)
hay DB\(\perp\)OB tại B
hay DB là tiếp tuyến của (O)

b: ΔOBC cân tại O có OE là đường cao
nên OE là phân giác của góc COB
Xét ΔBOE và ΔCOE có
OB=OC
góc BOE=góc COE
OE chung
=>ΔBOE=ΔCOE
=>góc OCE=góc OBE=90 độ
=>EC là tiếp tuyến của (O)
c: OB=OC
EB=EC
=>OE là trung trực của BC
=>sđ cung DB=sđ cung DC
=>góc BAD=góc CAD
=>AD là phân giác của góc BAC

Bạn tự vẽ hình giúp mình nha!
Ta có: OC=OB=R
Ta có: E là trung điểm BC
Suy ra: OE\(\perp\)CB
Tam giác OCB cân tại O, suy ra \(\widehat{OCB}=\widehat{OBC}\)
Ta có: \(\widehat{HCB}=\widehat{COD}\) (cùng phụ với góc \(\widehat{OCB}=\widehat{OBC}\))
Xét hai tam giác OCD và CHB, có:
\(\widehat{HCB}=\widehat{COD}\)
H và C là hai góc vuông
\(\Rightarrow\Delta OCD\sim\Delta CHB\)
\(\Rightarrow\dfrac{OC}{OD}=\dfrac{HC}{CB}\) \(\Leftrightarrow OC.OB=HC.OD\left(đccm\right)\)

a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=8(cm)
b: Xét ΔBOM và ΔAOM có
OB=OA
\(\widehat{BOM}=\widehat{AOM}\)
OM chung
Do đó: ΔBOM=ΔAOM
Suy ra: \(\widehat{OBM}=\widehat{OAM}=90^0\)
hay MA là tiếp tuyến của (O)

Ta có: Tam giác DAO cân tại O (vì OA = OD) => Góc ADO = Góc DAO
Ta lại có: Góc HBD = Góc ADO (cùng phụ Góc HDB) => Góc HBD = Góc DAO
Tam giác DBA vuông tại D => Góc DAB + Góc DBA = 90độ
Mà Góc DBA + Góc DBI = 90độ
=> Góc DAB = Góc DBI hay Góc DAO = Góc DBI
Từ 2 chứng minh trên ta được: Góc HBD = Góc DBI
=> BD (hay BK) là đường phân giác Góc HBI
Áp dụng tính chất đường phân giác vào tam giác BHI ta được:
KH / BH = KI / BI hay KH.BI = KI.BH (đpcm)
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
ΔOBC cân tại O
mà OE là trung tuyến
nên OE vuông góc với BC và OE là phân giác của góc BOC
b: Xét ΔOBD và ΔOCD có
OB=OC
góc BOD=góc COD
OD chung
Do đó: ΔOBD=ΔOCD
=>góc OBD=90 độ
=>DB là tiếp tuyên của (O)