cho tam giác ABC. Các điểm D,E,F theo thứ tự là trung điểm của BC, Ca,AB. Các điểm A',B',C' theo thứ tự là trung điểm của EF, DF, DE. Chứng minh rằng tam giác A'B'C' đồng dạng tam giác ABC.
Mọi người giúp mình với ạ^^
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 7 2017
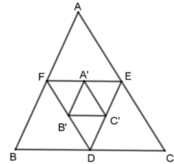
Vì D, E, F theo thứ tự làm trung điểm của BC, CA, AB nên EF, ED, FD là các đường trung bình của tam giác ABC nên E F B C = F D A C = E D A B = 1 2 suy ra ΔABC ~ ΔDEF (c - c - c) theo tỉ số đồng dạng k = 2.
Tương tự ta có A’B’, B’C’, C’A’ là các đường trung bình của tam giác DEF nên ΔA’B’C’ đồng dạng ΔDEF theo tỉ số k = 1 2
Theo tính chất đường trung bình B ' C E F = 1 2 mà E F B C = 1 2 (cmt) suy ra B ' C ' B C = 1 4
Tương tự A ' B ' A B = A ' C ' A C = 1 4
Do đó ΔA’B’C’ đồng dạng ΔABC theo tỉ số k = 1 4
Đáp án: C
12 tháng 5 2023
a: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
góc EAD=góc FAD
=>ΔAED=ΔAFD
=>AE=AF và DE=DF
=>AD là trung trực của EF
b: Sửa đề: ΔEKF
Xét ΔEKF có
FD là trung tuyến
FD=EK/2
=>ΔFEK vuông tại F