Chứng minh tổng ba góc trong một tam giác=90°
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
a) Ta dự đoán được sau khi ghép 3 góc nhọn đó sau khi ghép lại có tổng là \({180^o}\)
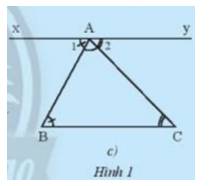
b) Qua A kẻ đường thẳng xy song song với BC
Ta có: xy // BC \( \Rightarrow \) \(\widehat B\) = \(\widehat {{A_1}}\) ( so le trong )
và \(\widehat C\) = \(\widehat {{A_2}}\)( so le trong )
Mà \(\widehat {{A_1}} + \widehat {BAC} + \widehat {{A_2}} = {180^o}\)
\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \) Tổng 3 góc trong 1 tam giác = \({180^o}\)
M
10 tháng 12 2017
A B C D M 1 2 1 1
a, Xét \(\Delta MAB-\Delta MDC:\)
\(\widehat{M_1}=\widehat{M_2}\)
\(AM=MD\left(gt\right)\)
\(BM=MC\left(gt\right)\)
\(\Rightarrow\)\(\Delta MAB=\Delta MDC\left(c.g.c\right)\)
b, Có \(\Delta MAB=\Delta MDC\left(cmt\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{D_1}\)
Hay AB // CD.
24 tháng 11 2021
a. B = 55 độ
C = 35
b. lỗi. phải là 360 độ
ông họ ngô
tôi họ đinh
CM
26 tháng 7 2018
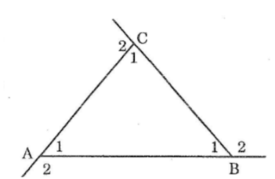
Ta có: ∠(A1 ) +∠(A2 ) =180o(hai góc kề bù)
∠(B1 ) +∠(B2 ) =180o(hai góc kề bù)
∠(C1 ) +∠(C2 )=180o(hai góc kề bù)
Suy ra: ∠(A1 ) +∠(A2 ) +∠(B1) +∠(B2 ) +∠(C1 ) +∠(C2 ) = 180º + 180º + 180º =540o
⇒∠(A2 ) + ∠( B2 ) +∠(C2 ) =540o-(∠(A1 ) +∠(B1 ) +∠(C1 ) ) (1)
Trong ΔABC, ta có:
∠(A1 ) +∠(B1 ) +∠(C1 ) =180o (tổng ba góc trong tam giác) (2)
Từ (1) và (2) suy ra: ∠(A2 ) +∠(B2 ) +∠(C2 ) =540o-180o=360o
TT
28 tháng 7 2015
Ta có tam giác ABC = 90 độ nên
góc ABC +góc ACB = 90 độ
vì lấy điểm E nằm trong tam giác nên
góc ABE + EBC + ACE + ECB = 90 độ
=> góc EBC + ECB < 90 độ
nên góc BEC > 90 độ
ON
27 tháng 10 2017
Ta có tam giác ABC = 90 độ nên
\(\widehat{ABC}+\widehat{ACE}=90^0\)
Vì lấy điểm E nằm trong tam giác nên\(\widehat{ABE}+\widehat{EBC}+\widehat{ACE}+\widehat{ECB}=90^0\)
\(\Rightarrow\)\(\widehat{EBC}+\widehat{ECB}< 90^0\); \(\widehat{EBC}+\widehat{ECB}< 90^0\)
Nên \(\widehat{BEC}>90^0\)
bạn ơi tổng ba góc trong một tm giác bằng 180 độ chứ ko phỉ 90 độ
bạn ghi đề s rồi