cho tam giác abc và các đường cao BH,CK
a) chứng minh tam giác ABH đồng dạng với tam giác ACK
b)Cho góc ACB= 40, Tính góc AKH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 4 2022
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔACK
b: Xét ΔKEB vuông tại K và ΔHEC vuông tại H có
\(\widehat{KEB}=\widehat{HEC}\)
DO đó: ΔKEB\(\sim\)ΔHEC
Suy ra: EK/EH=EB/EC
hay \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c: Xét ΔAKH và ΔACB có
AK/AC=AH/AB
góc A chung
Do đó: ΔAKH\(\sim\)ΔACB
Suy ra: \(\widehat{AKH}=\widehat{ACB}\)
2 tháng 4 2022
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔACK
b: Xét ΔKEB vuông tại K và ΔHEC vuông tại H có
\(\widehat{KEB}=\widehat{HEC}\)
DO đó: ΔKEB\(\sim\)ΔHEC
Suy ra: EK/EH=EB/EC
hay \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c: Xét ΔAKH và ΔACB có
AK/AC=AH/AB
góc A chung
Do đó: ΔAKH\(\sim\)ΔACB
Suy ra: \(\widehat{AKH}=\widehat{ACB}\)
D
27 tháng 1 2022
a) - Ta có: SABCD=AH.BC=AK.AB.
=>\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\)
- Ta có: \(\widehat{ABC}+\widehat{BAD}=180^0\) (AD//BC).
=>\(\widehat{ABC}+\widehat{BAH}+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(90^0+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(\widehat{HAK}+\widehat{KAD}=90^0\) mà \(\widehat{KAD}+\widehat{ADK}=90^0\) (tam giác ADK vuông tại K) nên \(\widehat{HAK}=\widehat{ADK}\) mà \(\widehat{ADK}=\widehat{ABC}\) (ABCD là hình bình hành) nên\(\widehat{HAK}=\widehat{ABC}\)
- Xét tam giác AKH và tam giác BCA có:
\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\) (cmt)
\(\widehat{HAK}=\widehat{ABC}\) (cmt)
=> Tam giác AKH ∼ Tam giác BCA (c-g-c).
b) - Ta có: Tam giác AKH ∼ Tam giác BCA (cmt) nên:
\(\widehat{AKH}=\widehat{ACB}=40^0\) (2 góc tương ứng)
28 tháng 2 2023
`a)`
Có `Delta ABC` cân tại `A=>AB=AC`
Xét `Delta ABH` và `Delta ACK` có :
`hat(AHB)=hat(AKC)(=90^0)`
`hat(A)-chung`
`AB=AC(cmt)`
`=>Delta ABH=Delota ACK(c.h-g.n)`
`b)`
Xét `Delta BHC` và `Delta CKB` có :
`hat(BHC)=hat(CKB)(=90^0)`
`hat(KBC)=hat(HCB)(hat(ABC)=hat(ACB))`
`BC-chung`
`=>Delta BHC=Delta CKB(c.h-g.n)`
`c)`
Có `Delta ABH= Delta ACK(cmt)=>AH=AK` ( 2 cạnh t/ứng )
`=>Delta AHK` cân tại `A=>hat(AHK)=(180^0-hat(A))/2`
`Delta ABC ` cân tại `A=>hat(ACB)=(180^0-hat(A))/2`
mà `2` góc này ở vị trí đ/vị
nên `KH//BC`
28 tháng 2 2023
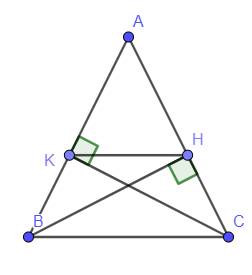
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K co
AB=AC
góc A chung
=>ΔAHB=ΔAKC
b: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
=>ΔKCB=ΔHBC
c: Xét ΔABC có AK/AB=AH/AC
nên KH//CB
22 tháng 3 2022
Xét tam giác AHB và tam giác AKC
^A _ chung ; AB = AC
Vậy tam giác AHB = tam giác AKC (ch-gn)
=> AH/AK = AB/AC => AH/AB = AK/AC
Xét tam giác AKH và tam giác ACB có
^A _ chung; AH/AB = AK/AC
Vậy tam giác AKH ~ tam giác ACB (c.g.c)
8 tháng 3 2021
a) Xét ΔABI vuông tại I và ΔACK vuông tại K có
\(\widehat{BAI}\) chung
Do đó: ΔABI\(\sim\)ΔACK(g-g)
27 tháng 1
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC
b: Ta có: ΔAHB=ΔAKC
=>AH=AK và \(\widehat{ABH}=\widehat{ACK}\)
Ta có: AH+HC=AC
AK+KB=AB
mà AH=AK và AC=AB
nen HC=KB
Xét ΔOKB vuông tại K và ΔOHC vuông tại H có
KB=HC
\(\widehat{KBO}=\widehat{HCO}\)
Do đó: ΔOKB=ΔOHC
c: ta có; ΔOKB=ΔOHC
=>OB=OC
=>O nằm trên đường trung trực của BC(1)
ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
ta có: IB=IC
=>I nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,O,I thẳng hàng