Chứng minh rằng -a phần b và a phần -b luôn bằng nhau,
-a phần -b và a phần b luôn bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
Đoàn Đức Hà
Giáo viên
20 tháng 7 2021
Đề: Cho \(\frac{a}{b}=\frac{c}{d}\). Chứng minh rằng: \(\frac{a}{b}=\frac{a+c}{b+d}=\frac{a-c}{b-d}\).
Giải:
Đặt \(\frac{a}{b}=\frac{c}{d}=t\).
\(\frac{a+c}{b+d}=\frac{bt+dt}{b+d}=\frac{t\left(b+d\right)}{b+d}=t\)
\(\frac{a-c}{b-d}=\frac{bt-dt}{b-d}=\frac{t\left(b-d\right)}{b-d}=t\)
Do đó \(\frac{a}{b}=\frac{a+c}{b+d}=\frac{a-c}{b-d}\).
DH
7 tháng 7 2017
Ta có:
\(\dfrac{a\dfrac{1}{b}}{b\dfrac{1}{a}}=\dfrac{\dfrac{ab+1}{b}}{\dfrac{ab+1}{a}}=\dfrac{ab+1}{b}.\dfrac{a}{ab+1}=\dfrac{a}{b}\)
Vậy...........
Chúc bạn học tốt!!!
14 tháng 2 2019
các phân số này bằng nhau là đương nhiên cái này là thi toán cấp huyện lớp 4
LA
6
27 tháng 10 2021
Áp dụng t.c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\\ \Leftrightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
BN
2
30 tháng 3 2020
Cho \(\frac{a}{b}=\frac{c}{d}\) chứng minh rằng \(\frac{a}{a-b}=\frac{c}{c-d}\)
Có \(\frac{a}{a-b}=\frac{c}{c-d}\Leftrightarrow\frac{a-b}{a}=\frac{c-d}{c}\Leftrightarrow\frac{a}{a}-\frac{b}{a}=\frac{c}{c}-\frac{d}{c}\Leftrightarrow1-\frac{b}{a}=1-\frac{d}{c}\)
\(\Rightarrow\frac{b}{a}=\frac{d}{c}hay\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\)
Đề bài cho \(\frac{a}{b}=\frac{c}{d}\) \(\Rightarrow b=c.\) Không thể \(ad=bc\Rightarrow\) Đề sai
30 tháng 3 2020
Ta có: \(\frac{a}{b}=\frac{c}{d}=k\left(k\ne0\right)\)
\(\Rightarrow a=kb,c=kd\)
Xét: \(\frac{a}{a-b}=\frac{bk}{bk-b}=\frac{bk}{b\left(k-1\right)}=\frac{k}{k-1}\left(1\right)\)
\(\frac{c}{c-d}=\frac{kd}{kd-d}=\frac{kd}{d\left(k-1\right)}=\frac{k}{k-1}\left(2\right)\)
Từ (1) và (2) => \(\frac{a}{a-b}=\frac{c}{c-d}\)
CM
2 tháng 6 2019
Ta có: (-a) . b = - (a . b) = a . (-b).
Do đó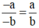 
(theo định nghĩa SGK).
vì mỗi số nguyên đề có hai giá trị.
a phần b nhân với -1 = -a phần -b
-a phần b nhân với -1 = a phần -b