Xác định hệ số a, b của hàm số y=ax + b biết đò thị hàm số đi qua điểm A(1;2) và song song với đường thẳng (d)
Giúp toii vớiiiii
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số y = ax + 3 là hàm số bậc nhất nên a ≠ 0
a) Đồ thị của hàm số đi qua điểm A(2; 6) nên:
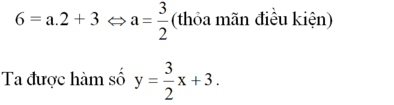
b) Vẽ đồ thị:
- Cho x = 0 thì y = 3 ta được B(0; 3).
Nối A, B ta được đồ thị hàm số

Lời giải:
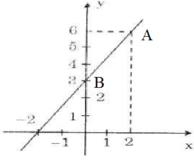
$(d)$ song song với $y=\frac{1}{2}x+1$ nên $a=\frac{1}{2}$
$A\in (d)$ nên:
$y_A=ax_A+b$
$\Leftrightarrow -2=a.2+b$
$\Leftrightarrow -2=\frac{1}{2}.2+b$
$\Leftrightarrow b=-3$
Vậy $a=\frac{1}{2}; b=-3$

b: Vì (d1)//(d) nên (d1): y=-2x+b
=>a=-2
Thay x=2 và y=1 vào (d1), ta được:
b-4=1
=>b=5
a: 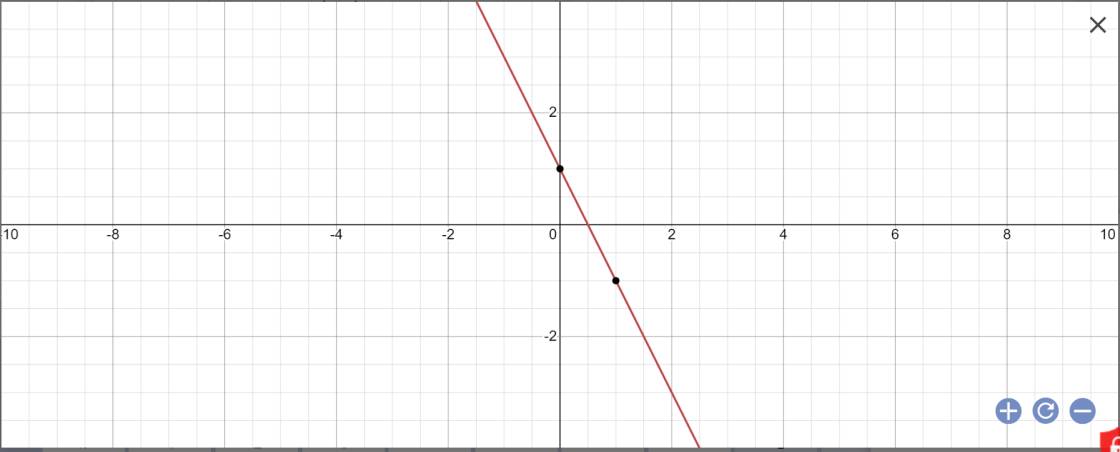

a, Đths đi qua \(A\left(-1;-3\right)\Leftrightarrow-3=-a+b\left(1\right)\)
Đths đi qua \(B\left(2;3\right)\Leftrightarrow3=2a+b\left(2\right)\)
\(\left(1\right)\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=-1\end{matrix}\right.\)
Vậy đths là \(y=2a-1\)
b, Đths đi qua \(M\left(-3;4\right)\Leftrightarrow4=-3a+b\left(1\right)\)
Đths song song với Ox \(\Leftrightarrow y=b=4\left(2\right)\)
\(\left(1\right)\left(2\right)\Leftrightarrow a=0\)
Vậy đths là \(y=4\)

\(a,\Leftrightarrow1-a=\dfrac{1}{2}\Leftrightarrow a=\dfrac{1}{2}\)
Hệ số góc: \(\dfrac{1}{2}\)
\(b,a=\dfrac{1}{2}\Leftrightarrow y=\dfrac{1}{2}x+1\)
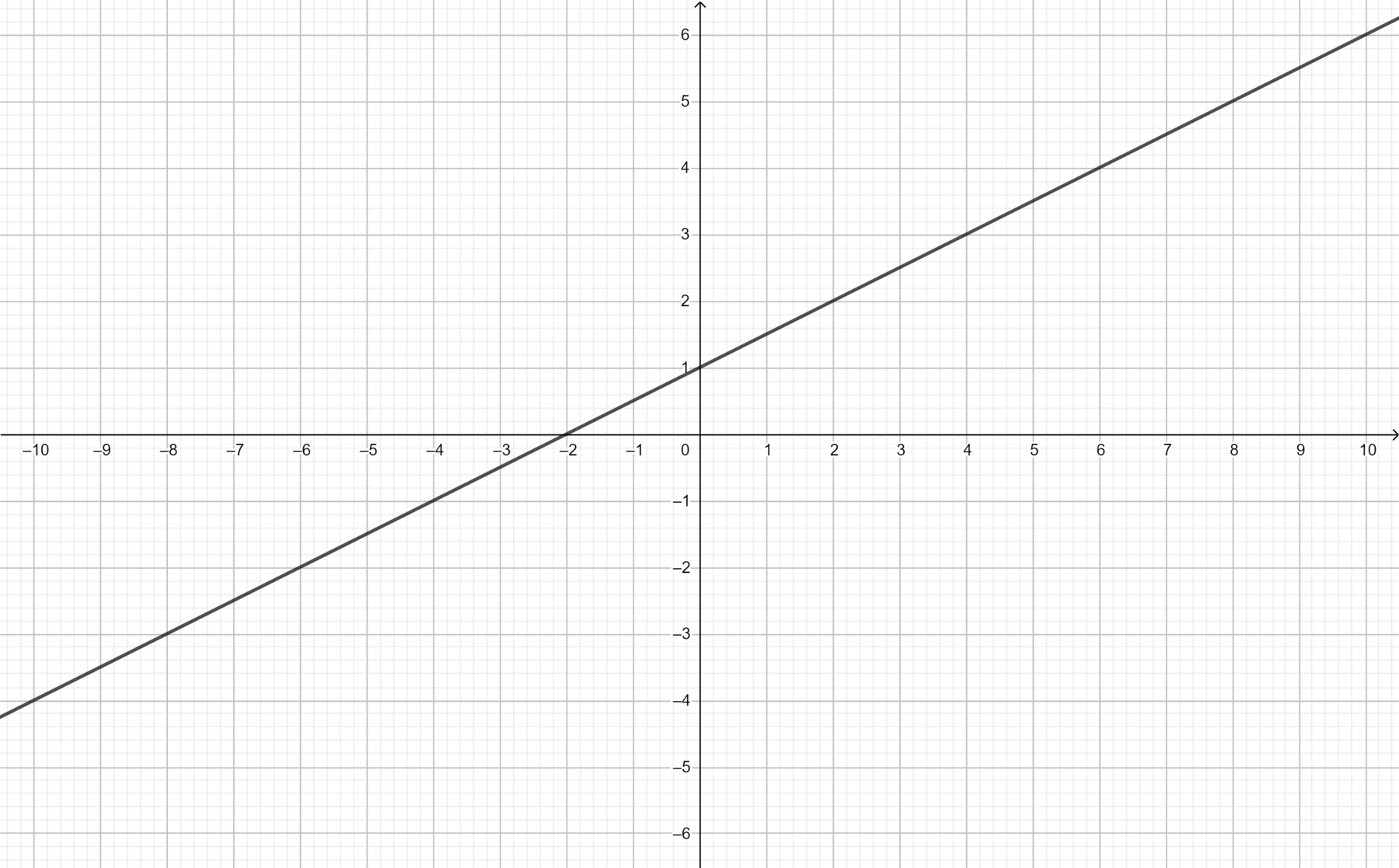

a: Thay x=-2 và y=6 vào (d), ta được:
-2a+4=6
=>-2a=2
=>a=2/-2=-1
b: a=-1 nên \(y=-x+4\)
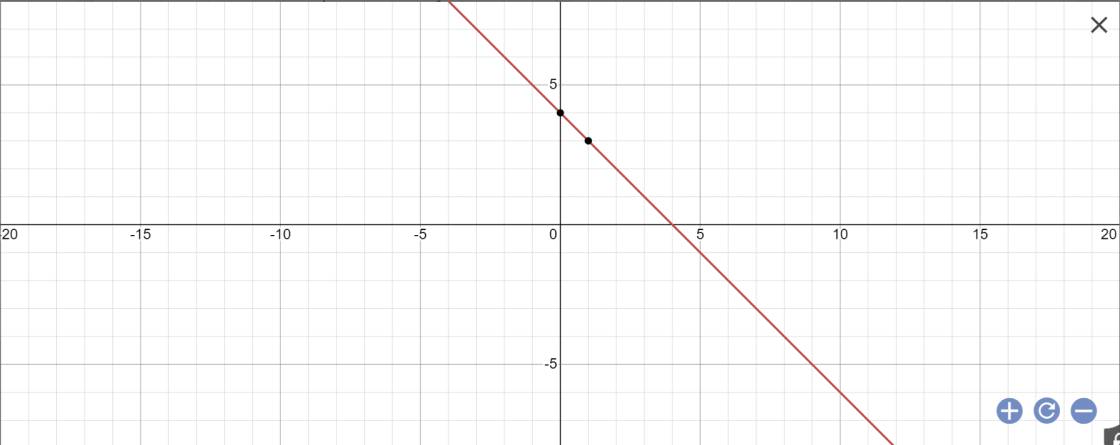
cho mình hỏi bạn có viết thiếu đề bài không ạ?