Một công ty TNHH trong một chiến dịch quảng cáo và bán sản phẩm mới dự kiến thuê xe để chở trên $140$ người và trên $9$ tấn hàng. Công ty tìm được nơi thuê xe có hai loại xe $A$ và $B$ đáp ứng yêu cầu. Trong đó xe loại $A$ có $10$ chiếc, xe loại $B$ có $9$ chiếc. Một chiếc xe loại $A$ cho thuê với giá $4$ triệu đồng, loại $B$ giá $3$ triệu đồng. Phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất? Biết rằng xe $A$ chỉ chở tối đa $20$ người và $0,6$ tấn hàng. Xe $B$ chở tối đa $10$ người và $1,5$ tấn hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

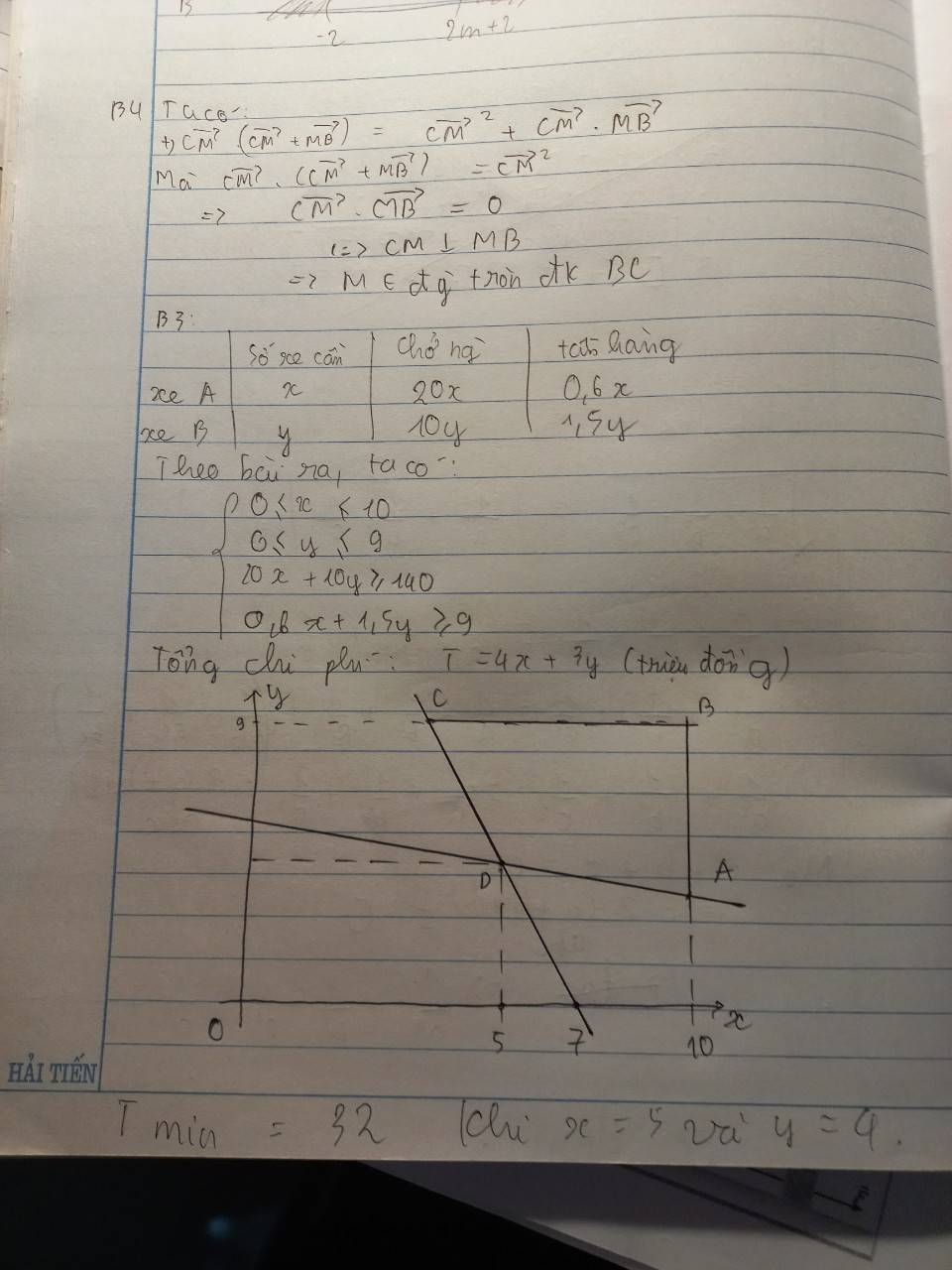

- Gọi số xe loại A và loại B cần dùng là x và y xe .
=> Số tiền là : \(T=4x+3y\)
Mà \(\left\{{}\begin{matrix}20x+10y\ge140\\0,6x+1,5y\ge9\end{matrix}\right.\) và \(\left\{{}\begin{matrix}x\ge0\\y\ge0\end{matrix}\right.\)
Ta có :

Chọn A
Gọi x; y lần lượt là số xe loại M, loại F cần thuê
Từ bài toán ta được hệ bất phương trình
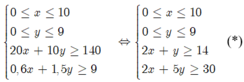
Tổng chi phí T(x; y) = 4x+ 3y (triệu đồng)
Bài toán trở thành là tìm x; y nguyên không âm thoả mãn hệ (*) sao cho T( ;xy) nhỏ nhất.
Từ đó ta cần thuê 5 xe hiệu M và 4 xe hiệu F thì chi phí vận tải là thấp nhất.

Đáp án 2 xe 8 tấn 2 xe 5 tấn 1 xe 2 tấn
Hoặc 1 xe 8 tấn 2 xe 5 tấn 5 xe 2 tấn

Cách 1: 1 xe 8 tấn, 2 xe 5 tấn, 5 xe 2 tấn
Cách 2: 2 xe 8 tấn, 2 xe 5 tấn, 1 xe 2 tấn
comment để biết thêm chi tiết.

C1:cả 3 chuyến chở 24 tấn còn còn 4 tấn thì 1 chuyến cuối thì chở 4 tấn
C2:1 xe 8 tấn , 2 xe 5 tấn , rời lại 2 xe 5 tấn
k hộ mình nhé

Gọi số xe ban đầu là x, x ∈ ℕ * (xe) nên số hàng theo kế hoạch mỗi xe chở là 24/x (tấn)
Số xe thực tế là x + 2 (xe) nên số hàng thực tế mỗi xe chở là 24/(x+2) (tấn)
Theo bài ra ta có phương trình:
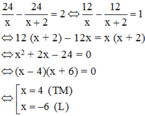
Vậy số xe ban đầu là 4 xe
Đáp án: A

Tham khảo:
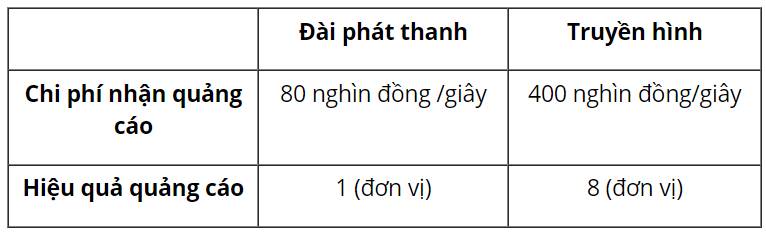
Gọi x và y là số giây quảng cáo trên đài phát thanh và trên truyền hình.
Khi đó \(x \ge 0;y \ge 0\)
160 triệu đồng=160000 (nghìn đồng)
Chi phí quảng cáo x giây trên đài phát thanh và y giây trên truyền hình là \(80x + 400y\)(nghìn đồng)
Vì công ty dự chi tối đa 160 triệu đồng nên ta có
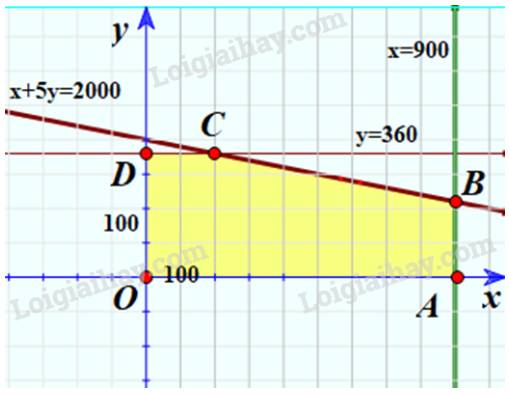
\(80x + 400y \le 160000\)\( \Leftrightarrow x + 5y \le 2000\)
Đài phát thanh chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 900 giây nên ta có: \(x \le 900\)
Đài truyền hình chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 360 giây nên ta có: \(y \le 360\)
Ta có hệ bất phương trình:
\(\left\{ {\begin{array}{*{20}{l}}
{x \ge 0}\\
{y \ge 0}\\
{x + 5y \le 2000}\\
{x \le 900}\\
{y \le 360}
\end{array}} \right.\)
Xác định miền nghiệm là miền ngũ giác OABCD với:
A(900;0); B(900;220); C(200;360); D(0;360)
Hiệu quả quảng cáo là: \(F\left( {x;y} \right) = x + 8y\)
Ta có:
\(F\left( {0;0} \right) = 0\)
\(F\left( {900;0} \right) = 900 + 8.0 = 900\)
\(F\left( {900;220} \right) = 900 + 8.220 = 2660\)
\(F\left( {200;360} \right) = 3080\)
\(F\left( {0;360} \right) = 2880\)
Vậy công ty cần đặt thời gian quảng cáo trên đài phát thanh là 200 giây và trên truyền hình là 360 giây thì hiệu quả nhất.
