cho điểm A nằm bên ngoài ( O;R), vẽ 2 tiếp tuyến AB, AC với đường tròn (O) (B, C là 2 tiếp điểm). Kẻ dây BD của đường tròn (O) và BD// OA
a) CMR: Bốn điểm A,O,B,C cùng thuộc 1 đường tròn
b) CMR: OA vuông góc với BC
c) CM: C,O,D thẳng hàng
d) Gọi E là giao điểm của AD và đường tròn (O, H là giao điểm của OA và BC. CMR góc AHE = góc OED rồi suy ra BC là tia phân giác của góc DHE
mn giải chi tiết giúp mk nhé! mk đang cần






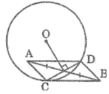

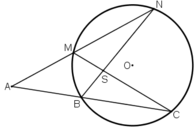

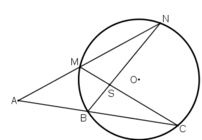

A B C O D E H
a/
\(AB\perp OA\Rightarrow\widehat{ABO}=90^o\)
\(AC\perp AO\Rightarrow\widehat{ACO}=90^o\)
=> B và C cùng nhìn AO dưới 1 góc \(90^o\) => B và C cùng nằm trên đường tròn đường kính AO hay A; O; B; C cùng nằm trên 1 đường tròn
b/
Xét tg vuông AOB và tg vuông ACO có
OB=OC=R
AB=AC (hai tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn)
=> tg ABO = tg ACO
Xét tg ABC có
AB=AC (cmt) => tg ABC cân tại A)
tg ABO = tg ACO \(\Rightarrow\widehat{OAB}=\widehat{OAC}\) => OA là phân giác của \(\widehat{BAC}\)
\(\Rightarrow OA\perp BC\) (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
c/ Nối O với C; O với D
BD//AO
\(AO\perp BC\) (cmt)
\(\Rightarrow BC\perp BD\Rightarrow\widehat{CBD}=90^o\)
Ta có
\(sđ\widehat{CBD}=\dfrac{1}{2}sđ\) cung BD (góc nội tiếp)
\(\Rightarrow sđ\) cung BC \(=2.sđ\widehat{CBD}=2.90^o=180^o\)
=> CD là đường kính của (O) => \(O\in CD\) => C; O; D thẳng hàng
d/