Bài 1: Cho đường tròn (O), đường kính AB, dây CD vuông góc với AB tại điểm H thuộc bán kính OA. Gọi M là điểm thuộc bán kính OB, E và F theo thứ tự là giao điểm của CM và DM với đường tròn (E khác C, F khác D). Chứng minh rằng: a) MC = MD b) ME = MFBài 2: Cho đường tròn (O) đường kính AB. Vẽ các dây BC, BD thuộc hai nửa mặt phẳng đối nhau bờ AB sao cho BD > BC. So sánh độ dài hai dây AD và AC.Bài 3....
Đọc tiếp
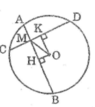
Bài 1: Cho đường tròn (O), đường kính AB, dây CD vuông góc với AB tại điểm H thuộc bán kính OA. Gọi M là điểm thuộc bán kính OB, E và F theo thứ tự là giao điểm của CM và DM với đường tròn (E khác C, F khác D). Chứng minh rằng: a) MC = MD b) ME = MF
Bài 2: Cho đường tròn (O) đường kính AB. Vẽ các dây BC, BD thuộc hai nửa mặt phẳng đối nhau bờ AB sao cho BD > BC. So sánh độ dài hai dây AD và AC.
Bài 3. Cho đường tròn (O), hai dây AB và AC vuông góc với nhau có độ dài theo thứ tự bằng 10cm và 24cm. a) Tính khoảng cách từ tâm đến mỗi dây b) chứng minh rằng ba điểm B, O, C thẳng hàng.
Bài 4. Cho đường tròn (O), hai dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm M nằm ngoài đường tròn. Trên tia đối của tia AB lấy điểm E sao cho AE = BM. Trên tia đối của tia CD lấy điểm F sao cho CF = DM. Chứng minh rằng OE = OF.
Bài 5. Cho đường tròn (O), hai dây AB và CD có AB > CD, các tia AB và CD cắt nhau tại điểm M nằm ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. So sánh các độ dài MH và MK.
giải giúp mình vs ạ . tạo mình đang cần gấp . cảm ơn nha

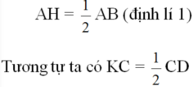
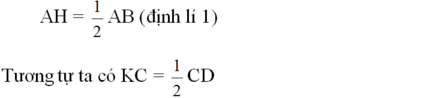
.png)
Lời giải chi tiết
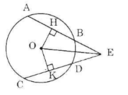
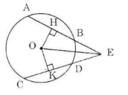
a) Nối OE.
Vì HA=HBHA=HB nên OH⊥ABOH⊥AB (ĐLí 2 - trang 103: đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
Vì KC=KDKC=KD nên OK⊥CDOK⊥CD. (ĐLí 2 - trang 103: đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
Mặt khác, AB=CDAB=CD nên OH=OKOH=OK (hai dây bằng nhau thì cách đều tâm).
Xét ΔHOEΔHOE và ΔKOEΔKOE có:
OH=OKOH=OK
EOEO chung
ˆEHO=ˆEKO=900EHO^=EKO^=900
Suy ra ΔHOE=ΔKOEΔHOE=ΔKOE (cạnh huyền - cạnh góc vuông)
Suy ra EH=EK(1)EH=EK(1)
b) Theo giả thiết, AB=CDAB=CD nên AB2=CD2AB2=CD2 hay AH=KCAH=KC (2)
Từ (1) và (2) suy ra EH+HA=EK+KCEH+HA=EK+KC
hay EA=EC.
a) Nối OE ta có: AB = CD
=> OH = OK (hai dây bằng nhau thì cách đều tâm)
H là trung điểm của AB nên OH ⊥ AB (đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
K là trung điểm của CD nên OK ⊥ CD (đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
Hai tam giác vuông OEH và OEK có:
OE là cạnh chung
OH = OK
Do đó ΔOEH = ΔOEK (cạnh huyền, cạnh góc vuông)
=> EH = EK (1). (đpcm)
b) Ta có: H là trung điểm của AB nên AH = \(\frac{1}{2}\)AB
K là trung điểm của CD nên CK = \(\frac{1}{2}\)CD
\(AH=\frac{1}{2}AB\)(định lí 1)
Tương tự ta có KC = \(\frac{1}{2}\)CD
Mà AB = CD (gt) suy ra AH = KC (2)
Từ (1) và (2) suy ra:
EA = EH + HA = EK + KC = EC
Vậy EA = EC. (đpcm)