cho tam giác ABC có diện tích là 143 cm2. Trên BC lấy điểm D sao cho BD=1/4 BC, trên AC lấy điểm E sao cho AE = 2/5 AC.Nối điểm D với E, biết M là trung điểm của DE. Tính diên tích hình tam giác ABM.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 6 2023
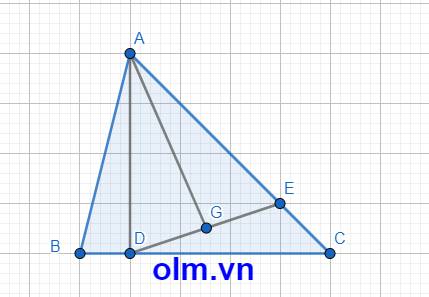
SADE = 2\(\times\)SAGE ( vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DE và DE = 2\(\times\) GE )
⇒ SADE = 36 \(\times\) 2 = 72 (cm2)
SADE = \(\dfrac{3}{4}\)\(\times\)SADC (vì hai tam giác có chung chiều cao hạ từ Đỉnh D xuống đáy AC và AE = \(\dfrac{3}{4}\)AC)
⇒ SACD = 72 : \(\dfrac{3}{4}\) = 96 (cm2)
DC = BC - BD = BC - \(\dfrac{1}{5}\)BC = \(\dfrac{4}{5}\)BC
SADC = \(\dfrac{4}{5}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và DC = \(\dfrac{4}{5}\)BC)
⇒ SABC = 96 : \(\dfrac{4}{5}\) = 120 (cm2)
Tỉ số phần trăm diện tích tam giác ADE và diện tích tam giác ABC là:
72 : 120 = 0,6
0,6 = 60%
Đáp số: 60%
18 tháng 1 2019
Ta có diện tích tam giác AEC=diện tích tam giác AGD(vì G là trung điểm của DE và có chung chiều cao )
Diện tích tam giác ADE là:
12+12=24cm
Ta có diện tích tam giác ECD=1/3 diện tích tam giác AED(vì CE=1/4AC và co chung cạnh đáy)
Diện tích tam giác ECD là:
24/4=8cm
Diện tích tam giác ACD là:
8+24=32cm
Diện tích tam giác ABC là:
32/2*3=48cm
Đáp số :48cm
2 tháng 3 2023
Kẻ đường cao AH
\(S_{ABD}=\dfrac{1}{2}\cdot AH\cdot BD;S_{ACD}=\dfrac{1}{2}\cdot AH\cdot CD\)
mà BD=CD
nên \(S_{ABD}=S_{ACD}=\dfrac{1}{2}\cdot180=90\left(cm^2\right)\)
Vì E là trung điểm của AC
nên \(S_{AED}=\dfrac{1}{2}\cdot90=45\left(cm^2\right)\)
Vì M là trung điểm của DE
nên \(S_{AME}=\dfrac{1}{2}\cdot45=22.5\left(cm^2\right)\)