Cho hình thoi ABCD. Trên tia đối của BA lấy điểm M, trên tia đối của CB lấy điểm N, trên tia đối của DC lấy điểm P và trên tia đối của AD lấy điểm Q sao cho BM = CN = DP = AQ . a. CM : MNPQ là hình bì...

LV

Lò Văn Phú

29 tháng 11 2022 - olm

Cho hình thoi ABCD. Trên tia đối của BA lấy điểm M, trên tia đối của CB lấy điểm N, trên tia đối của DC lấy điểm P và trên tia đối của AD lấy điểm Q sao cho BM = CN = DP = AQ . a. CM : MNPQ là hình bình hành b. CM : hình bình hành MNPQ và hình thoi ABCD có cùng 1 tâm đối xứng c. Hình thoi ABCD có điều kiện gì để MNPQ là hình vuông...

Đọc tiếp

#Toán lớp 8

0

NV

Nguyễn Vy Khanh

27 tháng 11 2018 - olm

Cho hình thoi ABCD . Trên tia đối của tia BA lấy M,trên tia đối của CB lấy N,trên tia đối của DC lấy P,trên tia đối của AD lấy Q sao cho BM=CN=DP=AQ

a) CM tứ giác MNPQ và BMPQ là hình bình hành

b) CM ABCD và MNPQ có chung tâm đối xứng

#Toán lớp 8

0

TP

thuthao pham

29 tháng 8 2017 - olm

Cho hình thoi ABCD. Trên tia đối của tia BA lấy điểm M, trên tia đối của tia CB lấy điểm N, trên tia đối của tia DC lấy điểm T, trên tia đối của tia AD lấy Q sao cho: BM=CN=DB=AQ.

a, CM:tứ giác MNPQ là hình bình hành

b, CMR: hình bình hành MNPQ là hình thang có tâm đối xứng

c, Nếu ABCD là hình vuông thì tứ giác MNPQ là hình gì , vì sao ?

#Toán lớp 8

0

MS

My Sunshine

15 tháng 10 2016

cho hình thoi ABCD.trên tia đối của tia BA lấy điểm M,trên tia đối của tia CB lấy điểm N,trên tia đối của tia DC lấy điểm P và trên tia đối của tia AD lấy điểm Qsao cho BM=CN=DP=AQ

a) chứng minh tứ giác MNPQ là hình bình hành

b) chứng minh AC,BD,MP,NQ đồng quy tại một điểm

#Toán lớp 8

0

PT

Pham Trong Bach

13 tháng 3 2018

Cho hình vuông ABCD có AB = 3cm

Trên tia đối của tia BA lấy điểm K sao cho BK = 1cm

Trên tia đối của tia CB lấy điểm L sao cho CL = 1cm

Trên tia đối của tia DC lấy điểm M sao cho MD = 1cm

Trên tia đối của tia AD lấy điểm N sao cho NA = 1cm

Chứng minh KLMN là hình vuông

#Toán lớp 8

1

CM

Cao Minh Tâm

13 tháng 3 2018

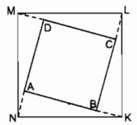
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Xét △ ANK và △ BKL :

AN = BK (gt)

∠ A = ∠ B = 90 0

AK = BL (vì AB = BC, BK = CL)

Do đó △ ANK = △ BKL (c.g.c)

⇒ NK = KL (1)

Xét △ BKL và △ CLM:

BK = CL (gt)

∠ B = ∠ C = 90 0

BL = CM (vì BC = CD, CL = DM)

Do đó: △ BKL = △ CLM (c.g.c)

⇒ KL = LM (2)

Xét △ CLM và △ DMN :

CL = DM (gt)

∠ C = ∠ D = 90 0

CM = DN (vì CD = DA, DM = AN)

Do đó: △ CLM = △ DMN (c.g.c)

⇒ LM = MN (3)

Từ (1), (2) và (3) ⇒ NK = KL = LM = MN

Tứ giác MNKL là hình thoi

△ ANK = △ BKL ⇒ ∠ (ANK) = ∠ (BKL)

Trong tam giác ANK có A là góc vuông ⇒ ∠ (ANK) + ∠ (AKN) = 90 0

⇒ ∠ (BKL) + ∠ (AKN) = 90 0 hay ∠ (NKL) = 90 0

Vậy tứ giác MNKL là hình vuông.

Đúng(0)

BH

bùi huyền trang

19 tháng 11 2019 - olm

cho hình thoi ABCD, trên tia đôi các tia BA, CB, DC, AD lần lượt lấy M, N, P, Q. sao cho BM = CN = DP = AQ

a) CMR: tứ giác MNPQ và hình thoi ABCD có chung tâm đối xứng

b) Nếu ABCD là hình vuông thì tứ giác MNPQ là hình gì?

#Toán lớp 8

0

SG

Sách Giáo Khoa

29 tháng 4 2017

Cho hình vuông ABCD có AB = 3cm

Trên tia đối của tia BA lấy điểm K sao cho BK = 1cm

Trên tia đối của tia CB lấy điểm L sao cho CL = 1cm

Trên tia đối của tia DC lấy điểm M sao cho MD = 1cm

Trên tia đối của tia AD lấy điểm N sao cho NA = 1cm

Chứng minh KLMN là hình vuông

#Toán lớp 8

1

NT

Nguyen Thuy Hoa

1 tháng 7 2017

Đa giác. Đa giác đều

Đúng(0)

GH

Giang Hoàng Gia Linh

3 tháng 10 2023

Bài 19. Cho hình thoi ABCD. Trên tia đối của tia BA lấy điểm E, trên tia đối của tiaCB lấy điểm F, trên ta đối của tia DC lấy điểm G, trên tia đối của tia AD lấyđiểm H sao cho BE = CF = DG = AH.1. Chứng minh tứ giác EF GH là hình bình hành.2. Chứng minh hình bình hành EF GH và hình thoi ABCD có chung tâm đốixứng.3. Nếu ABCD là hình vuông thì EF GH là hình gì? Tại...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

10 tháng 12 2023

1:

ta có:ABCD là hình thoi

=>\(\widehat{BAD}=\widehat{BCD};\widehat{ABC}=\widehat{ADC}\)

Ta có: \(\widehat{BAD}+\widehat{EAH}=180^0\)(hai góc kề bù)

\(\widehat{BCD}+\widehat{FCD}=180^0\)(hai góc kề bù)

mà \(\widehat{BAD}=\widehat{BCD}\)

nên \(\widehat{EAH}=\widehat{FCD}\)

Ta có: \(\widehat{ABC}+\widehat{EBC}=180^0\)(hai góc kề bù)

\(\widehat{ADC}+\widehat{ADG}=180^0\)(hai góc kề bù)

mà \(\widehat{ABC}=\widehat{ADC}\)

nên \(\widehat{EBC}=\widehat{ADG}\)

Ta có: \(DA+AH=DH\)

\(AB+BE=AE\)

\(BC+CF=BF\)

\(CD+DG=CG\)

mà DA=AB=BC=CD và AH=BE=CF=DG

nên DH=AE=BF=CG

Xét ΔHAE và ΔFCG có

HA=FC

\(\widehat{HAE}=\widehat{FCG}\)

AE=CG

Do đó: ΔHAE=ΔFCG

=>HE=FG

Xét ΔHDG và ΔFBE có

DH=BF

\(\widehat{HDG}=\widehat{BFE}\)

DG=BE

Do đó: ΔHDG=ΔFBE

=>HG=FE

Xét tứ giác GHEF có

GH=EF

GF=HE

Do đó: GHEF là hình bình hành

2: Gọi O là giao điểm của AC và BD

Ta có: ABCD là hình thoi

=>AC cắt BD tại trung điểm của mỗi đường

=>O là trung điểm chung của AC và BD

Xét tứ giác AHCF có

AH//CF

AH=CF

Do đó: AHCF là hình bình hành

=>AC cắt HF tại trung điểm của mỗi đường

mà O là trung điểm của AC

nên O là trung điểmcủa HF

Ta có: EHGF là hình bình hành

=>EG cắt HF tại trung điểm của mỗi đường

mà O là trung điểm của HF

nên O là trung điểm của EG

=>Hình bình hành EHGF và hình thoi ABCD có chung tâm

Đúng(0)

GH

Giang Hoàng Gia Linh

7 tháng 10 2023

Bài 19. Cho hình thoi ABCD. Trên tia đối của tia BA lấy điểm E, trên tia đối của tiaCB lấy điểm F, trên ta đối của tia DC lấy điểm G, trên tia đối của tia AD lấyđiểm H sao cho BE = CF = DG = AH.1. Chứng minh tứ giác EF GH là hình bình hành.2. Chứng minh hình bình hành EF GH và hình thoi ABCD có chung tâm đốixứng.3. Nếu ABCD là hình vuông thì EF GH là hình gì? Tại...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

7 tháng 10 2023

1: DH=DA+AH

CG=CD+DG

BF=BC+CF

AE=AB+BE

mà DA=CD=BC=AB và AH=DG=CF=BE

nên DH=CG=BF=AE

góc ADG=180 độ-góc ADC

góc EBF=180 độ-góc ABC

mà góc ADC=góc ABC

nên góc ADG=góc EBF

góc EAB=180 độ-góc BAD

góc GCF=180 độ-góc BCD

mà góc BAD=góc BCD

nên góc EAB=góc GCF

Xét ΔHDG và ΔFBE có

HD=FB

góc HDG=góc FBE

DG=BE

Do đó: ΔHDG=ΔFBE

=>HG=FE

Xét ΔHAE và ΔFCG có

HA=FC

góc HAE=góc FCG

AE=CG

Do đó: ΔHAE=ΔFCG

=>HE=FG

Xét ΔADG và ΔCBE có

AD=CB

góc ADG=góc CBE

DG=BE

Do đó: ΔADG=ΔCBE

=>AG=CE

Xét tứ giác EHGF có

EH=FG

EF=GH

Do đó: EHGF là hình bình hành

2:

Gọi O là giao của AC và BD

ABCD là hình thoi

=>AC cắt BD tại trung điểm của mỗi đường

=>O là trung điểm chung của AC và BD

Xét tứ giác AGCE có

AG=CE

AE=CG

Do đó: AGCE là hình bình hành

=>AC cắt GE tại trung điểm của mỗi đường

=>O là trung điểm của GE

GHEF là hình bình hành

=>GE cắt HF tại trung điểm của mỗi đường

=>O là trung điểm của HF

=>ĐPCM

3:

ABCD là hình vuông

=>góc BAD=góc ADC=90 độ

Xét ΔHAE vuông tại A và ΔGDH vuông tại D có

HA=GD

AE=DH

Do đó: ΔHAE=ΔGDH

=>HE=GH

Xét hình bình hành EHGF có HE=GH

nên EHGF là hình thoi

Đúng(1)

NL

Nguyễn Lê Trung Nguyên

27 tháng 7 2017 - olm

Cho hình bình hành ABCD. Trên tia đối của tia Ad và CB lấy điểm M và N sao cho AM=CP. Trên tia đối của tia BA và DC lấy các điểm N và Q sao cho BN=DQ. CMR: MP, NQ, AC và BQ đồng quy

#Toán lớp 8

0

NH

Nguyen Huong

6 tháng 9 2018 - olm

Cho hình bình hành ABCD. Trên tia đối của tia Ad và CB lấy điểm M và N sao cho AM=CP. Trên tia đối của tia BA và DC lấy các điểm N và Q sao cho BN=DQ. CMR: MP, NQ, AC và BQ đồng quy

#Toán lớp 8

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP