\(\sqrt{20}-\sqrt{21-4\sqrt{5}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 7 2023
`sqrt(20)-sqrt(21-4sqrt5)=2\sqrt5-sqrt((2\sqrt5)^2-2.2sqrt5 .1+1^2)=2\sqrt5-sqrt((2sqrt5-1)^2)=2sqrt5-2sqrt5+1=1`
1 tháng 7 2023
`@` `\text {Ans}`
`\downarrow`
`\sqrt {20} -` \(\sqrt {21 - 4 \sqrt {5}}\)
`= 2 \sqrt {5} - \sqrt {20 + 1 - 4 \sqrt {5}}`
`= 2 \sqrt {5} - \sqrt {(2\sqrt {5})^2 - 2*2 \sqrt {5} + 1}`
`= 2 \sqrt {5} - \sqrt {(2 \sqrt {5} - 1)^2}`
`= 2 \sqrt {5} - 2 \sqrt {5} + 1`
`= 1`
14 tháng 10 2021
\(a,\left(\sqrt{2}+\sqrt{11}\right)^2=12+2\sqrt{22}\\ \left(\sqrt{3}+5\right)^2=28+10\sqrt{3}\)
Ta thấy \(12< 28;2\sqrt{22}=\sqrt{88}< \sqrt{300}=10\sqrt{3}\)
Nên \(\sqrt{2}+\sqrt{11}< \sqrt{3}+5\)
\(b,\left(\sqrt{21}-\sqrt{5}\right)^2=26-2\sqrt{105}\\ \left(\sqrt{20}-\sqrt{6}\right)^2=26-2\sqrt{120}\)
Vì \(\sqrt{105}< \sqrt{120}\Rightarrow-2\sqrt{105}>-2\sqrt{120}\)
Nên \(\sqrt{21}-\sqrt{5}>\sqrt{20}-\sqrt{6}\)
6 tháng 6 2021
Bài 2:
a)\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\) (đk: \(x\ge2\))
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9\left(x-2\right)}+\dfrac{6}{\sqrt{81}}\sqrt{x-2}=-4\)
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-2\sqrt{x-2}+\dfrac{2}{3}\sqrt{x-2}=-4\)
\(\Leftrightarrow-\sqrt{x-2}=-4\) \(\Leftrightarrow x-2=16\)
\(\Leftrightarrow x=18\) (thỏa)
Vậy...
b)\(\sqrt{9x^2+12x+4}=4x\)(Đk:\(9x^2+12x+4\ge0\))
\(\Leftrightarrow\left\{{}\begin{matrix}4x\ge0\\9x^2+12x+4=16x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+12x+4=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+14x-2x+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(x-2\right)\left(-7x-2\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x=2\\x=-\dfrac{2}{7}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x=2\) (tm đk)
Vậy...
c) \(\sqrt{x-2\sqrt{x-1}}=\sqrt{x-1}\) (đk: \(x\ge1\))
\(\Leftrightarrow x-2\sqrt{x-1}=x-1\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{1}{2}\) \(\Leftrightarrow x=\dfrac{5}{4}\) (tm)
Vậy...
H9
HT.Phong (9A5)
CTVHS
17 tháng 7 2023
1) \(\sqrt{6+4\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{2^2+2\cdot2\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{3^2-2\cdot3\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(2+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}\)
\(=\left|2+\sqrt{2}\right|-\left|3-\sqrt{2}\right|\)
\(=2+\sqrt{2}-3+\sqrt{2}\)
\(=2\sqrt{2}-1\)
2) \(\sqrt{21-4\sqrt{5}}+\sqrt{21+4\sqrt{5}}\)
\(=\sqrt{20-4\sqrt{5}+1}+\sqrt{20+4\sqrt{5}+1}\)
\(=\sqrt{\left(2\sqrt{5}\right)^2-2\sqrt{5}\cdot2\cdot1+1^2}+\sqrt{\left(2\sqrt{5}\right)^2+2\sqrt{5}\cdot2\cdot1-1^2}\)
\(=\sqrt{\left(2\sqrt{5}-1\right)^2}+\sqrt{\left(2\sqrt{5}+1\right)^2}\)
\(=\left|2\sqrt{5}-1\right|+\left|2\sqrt{5}+1\right|\)
\(=2\sqrt{5}-1+2\sqrt{5}+1\)
\(=4\sqrt{5}\)
AT
8 tháng 7 2021
i) \(\sqrt{8-3\sqrt{7}}+\sqrt{4-\sqrt{7}}=\sqrt{\dfrac{16-6\sqrt{7}}{2}}+\sqrt{\dfrac{8-2\sqrt{7}}{2}}\)
\(=\sqrt{\dfrac{\left(3-\sqrt{7}\right)^2}{2}}+\sqrt{\dfrac{\left(\sqrt{7}-1\right)^2}{2}}=\dfrac{\left|3-\sqrt{7}\right|}{\sqrt{2}}+\dfrac{\left|\sqrt{7}-1\right|}{\sqrt{2}}\)
\(=\dfrac{3-\sqrt{7}}{\sqrt{2}}+\dfrac{\sqrt{7}-1}{\sqrt{2}}=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
j) \(\sqrt{5+\sqrt{21}}-\sqrt{5-\sqrt{21}}=\sqrt{\dfrac{10+2\sqrt{21}}{2}}-\sqrt{\dfrac{10-2\sqrt{21}}{2}}\)
\(=\sqrt{\dfrac{\left(\sqrt{7}+\sqrt{3}\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{7}-\sqrt{3}\right)^2}{2}}=\dfrac{\left|\sqrt{7}+\sqrt{3}\right|}{\sqrt{2}}-\dfrac{\left|\sqrt{7}-\sqrt{3}\right|}{\sqrt{2}}\)
\(=\dfrac{\sqrt{7}+\sqrt{3}}{\sqrt{2}}-\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{2}}=\dfrac{2\sqrt{3}}{\sqrt{2}}=\sqrt{6}\)
20 tháng 6 2021
`a)A=(3-sqrt5)sqrt{3+sqrt5}+(3+sqrt5)sqrt{3-sqrt5}`
`=sqrt{3-sqrt5}sqrt{3+sqrt5}(sqrt{3+sqrt5}+sqrt{3-sqrt5})`
`=sqrt{9-5}(sqrt{3+sqrt5}+sqrt{3-sqrt5})`
`=2(sqrt{3+sqrt5}+sqrt{3-sqrt5})`
`=sqrt2(sqrt{6+2sqrt5}+sqrt{6-2sqrt5})`
`=sqrt2(sqrt{(sqrt5+1)^2}+sqrt{(sqrt5+1)^2})`
`=sqrt2(sqrt5+1+sqrt5-1)`
`=sqrt{2}.2sqrt5`
`=2sqrt{10}`
20 tháng 6 2021
`b)B=(5+sqrt{21})(sqrt{14}-sqrt6)sqrt{5-sqrt{21}}`
`=sqrt{5+sqrt{21}}sqrt{5-sqrt{21}}sqrt{5+sqrt{21}}(sqrt{14}-sqrt6)`
`=sqrt{25-21}sqrt{5+sqrt{21}}(sqrt{14}-sqrt6)`
`=2sqrt{5+sqrt{21}}(sqrt{14}-sqrt6)`
`=2sqrt2sqrt{5+sqrt{21}}(sqrt{7}-sqrt3)`
`=2sqrt{10+2sqrt{21}}(sqrt{7}-sqrt3)`
`=2sqrt{(sqrt3+sqrt7)^2}(sqrt{7}-sqrt3)`
`=2(sqrt3+sqrt7)(sqrt{7}-sqrt3)`
`=2(7-3)`
`=8`
`c)C=sqrt{4+sqrt7}-sqrt{4-sqrt7}`
`=sqrt{(8+2sqrt7)/2}-sqrt{(8-2sqrt7)/2}`
`=sqrt{(sqrt7+1)^2/2}-sqrt{(sqrt7+1)^2/2}`
`=(sqrt7+1)/sqrt2-(sqrt7-1)/2`
`=2/sqrt2=sqrt2`
30 tháng 8 2018
Câu a : \(\left(\sqrt{80}+\sqrt{20}\right):\sqrt{45}=\sqrt{80}:\sqrt{45}+\sqrt{20}:\sqrt{45}=\sqrt{\dfrac{16}{9}}+\sqrt{\dfrac{4}{9}}=\dfrac{4}{3}+\dfrac{2}{3}=\dfrac{6}{3}=2\)
Câu b : \(\left(\sqrt{3}-\sqrt{2}\right)\left(\sqrt{18}+\sqrt{27}\right)=\sqrt{54}+\sqrt{81}-\sqrt{36}-\sqrt{54}=\sqrt{81}-\sqrt{36}=9-6=3\)
Câu c : \(\dfrac{5\sqrt{3}-3\sqrt{5}}{\sqrt{5}-\sqrt{3}}-\dfrac{6}{\sqrt{15+3}}=\dfrac{\sqrt{15}\left(\sqrt{5}-\sqrt{3}\right)}{\sqrt{5}-\sqrt{3}}-\dfrac{6}{\sqrt{18}}\)
\(=\sqrt{15}-\dfrac{6}{\sqrt{18}}=\dfrac{\sqrt{270}-6}{3\sqrt{2}}=\dfrac{3\sqrt{30}-6}{3\sqrt{2}}=\dfrac{3\left(\sqrt{30}-6\right)}{3\sqrt{2}}=\dfrac{\sqrt{30}-2}{\sqrt{2}}=\sqrt{15}-\sqrt{2}\)
CS
20 tháng 10 2021
a) \(=2\sqrt{5}-3\sqrt{5}+\sqrt{5}-1=-1\)
b) \(=\left[\sqrt{14}+\dfrac{\sqrt{6}\left(\sqrt{2}+\sqrt{5}\right)}{\sqrt{2}+\sqrt{5}}\right].\sqrt{\left(\sqrt{\dfrac{7}{2}}-\sqrt{\dfrac{3}{2}}\right)^2}\)
\(=\left(\sqrt{14}+\sqrt{6}\right)\left(\sqrt{\dfrac{7}{2}}-\sqrt{\dfrac{3}{2}}\right)\)
\(=\sqrt{49}-\sqrt{21}+\sqrt{21}-\sqrt{9}\)
\(=7-3=4\)
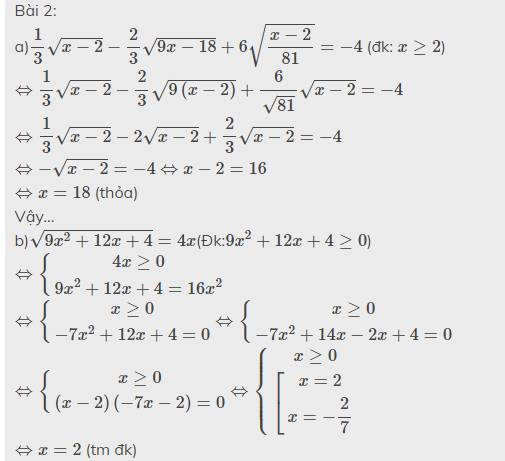
Lời giải:
$\sqrt{20}-\sqrt{21-4\sqrt{5}}=\sqrt{20}-\sqrt{20+1-2\sqrt{20}}=\sqrt{20}-\sqrt{(\sqrt{20}-1)^2}=\sqrt{20}-|\sqrt{20}-1|=\sqrt{20}-(\sqrt{20}-1)=1$