tìm nghiệm của đa thức x^2 -5x+4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
3 tháng 10 2019
Đa thức f(x) = x2 – 5x + 4 có dạng ax2 + bx+ c trong đó hệ số a = 1, b = -5, c = 4
Ta có: a + b + c = 1 + (-5) + 4 = 1 – 5 + 4 = 0
Theo bài 46, vì a + b + c = 0 nên đa thức f(x) = x2 – 5x + 4 có nghiệm x = 1
T
3
C
14 tháng 3 2023
`x^2 - 3x = 0`
`<=> x.(x-3)=0`
`<=> x = 0` hoặc `x-3=0`
`<=> x = 0 ` hoặc `x = 3`
Vậy `S = { 0;3}`
`2x^2 + 5x = 0`
`<=> x.(2x + 5)=0`
`<=> x = 0` hoặc `2x+5=0`
`<=> x = 0` hoặc `2x= -5`
`<=> x = 0` hoặc `x = -5/2`
Vậy `S = {0; -5/2}`
14 tháng 3 2023
\(a,x^2-3x=0\\ x\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\\ b,2x^2+5x=0\\ x\left(2x+5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\2x+5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{2}\end{matrix}\right.\)
KK
3
11 tháng 4 2023
Phân tích đa thức thành nhân tử thôi bạn :
Ta có :
\(h\left(x\right)=x^2+5x+6\)
\(h\left(x\right)=x\left(x+2\right)+3\left(x+2\right)\)
\(h\left(x\right)=\left(x+2\right)\left(x+3\right)\)
\(\Rightarrow N_oh\left(x\right)=-2;-3\)
\(g\left(x\right)=2x^2+7x-9\)
\(g\left(x\right)=2x^2+9x-2x-9\)
\(g\left(x\right)=2x\left(x-1\right)+9\left(x-1\right)\)
\(g\left(x\right)=\left(x-1\right)\left(2x+9\right)\)
\(\Rightarrow N_og\left(x\right)=1;-4,5\)
30 tháng 4 2019
Ta có f(x)=0f(x)=0
⇔x2−5x+4=0⇔x2−5x+4=0
⇔x2−4x−x+4=0⇔x2−4x−x+4=0
⇔x(x−4)−(x−4)=0⇔x(x−4)−(x−4)=0
⇔(x−1)(x−4)=0⇔(x−1)(x−4)=0
⇔x=1⇔x=1 hoặc x=4x=4
Vậy: . . .
b) f(x) = 2x2x2 + 3x + 1
Ta có f(x)=0f(x)=0
⇔2x2+3x+1=0⇔2x2+3x+1=0
⇔2x2+2x+x+1=0⇔2x2+2x+x+1=0
⇔2x(x+1)+(x+1)=0⇔2x(x+1)+(x+1)=0
⇔(x+1)(2x+1)=0⇔(x+1)(2x+1)=0
⇔x=−1⇔x=−1 hoặc x=−12x=−12
Vậy: . . .
T
30 tháng 4 2019
a, Để \(x\) là nghiệm của \(f\left(x\right)\)thì:
\(x^2-5x+4=0\)
\(\Leftrightarrow x^2-x-\left(4x+4\right)=0\)
\(\Leftrightarrow x\left(x-1\right)+4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x+4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=-4\end{cases}}}\)
Vậy \(x=1,x=-4\)là hai nghiệm của \(f\left(x\right)\)
b, Để \(x\)là nghiệm của \(f\left(x\right)\)thì:
\(2x^2+3x+1=0\)
\(\Leftrightarrow2x^2+2x+x+1=0\)
\(\Leftrightarrow2x\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\2x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0-1\\2x=-1\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-1\\x=\frac{-1}{2}\end{cases}}}\)
Vậy \(x=-1,x=\frac{-1}{2}\)là nghiệm của \(f\left(x\right)\)
TC
13 tháng 4 2022
cho B(x) = 0
\(=>-5x+30=0\Rightarrow-5x=-30\Rightarrow x=6\)
cho E(x) = 0
\(=>x^2-81=0\Rightarrow x^2=81=>\left[{}\begin{matrix}x=9\\x=-9\end{matrix}\right.\)
cho C(x) = 0
\(=>2x+\dfrac{1}{3}=0=>2x=-\dfrac{1}{3}=>x=-\dfrac{1}{6}\)
13 tháng 4 2022
bạn tham khảo hai câu này nha vì mình ko biết là mấy câu còn lại
B(x)=-5x+30
cho B(x)=0
=> -5x+30=0
-5x=-30
x=-30:(-5)
x=-6
* Vậy nghiệm của đa thức B(x) là -6.
C(x)=2x+1/3
cho C(x)=0
=>2x+1/3=0
2x=-1/3
x=-1/3:2
x=-1/6
vậy nghiệm của đa thức C(x) là -1/6.
21 tháng 6 2023
a: f(x)=x^3-2x^2+2x-5
g(x)=-x^3+3x^2-2x+4
b: Sửa đề: h(x)=f(x)+g(x)
h(x)=x^3-2x^2+2x-5-x^3+3x^2-2x+4=x^2-1
c: h(x)=0
=>x^2-1=0
=>x=1 hoặc x=-1
AH
Akai Haruma
Giáo viên
23 tháng 5 2021
Lời giải:
1.
$4x+9=0$
$4x=-9$
$x=\frac{-9}{4}$
2.
$-5x+6=0$
$-5x=-6$
$x=\frac{6}{5}$
3.
$x^2-1=0$
$x^2=1=1^2=(-1)^2$
$x=\pm 1$
4.
$x^2-9=0$
$x^2=9=3^2=(-3)^2$
$x=\pm 3$
AH
Akai Haruma
Giáo viên
23 tháng 5 2021
5.
$x^2-x=0$
$x(x-1)=0$
$x=0$ hoặc $x-1=0$
$x=0$ hoặc $x=1$
6.
$x^2-2x=0$
$x(x-2)=0$
$x=0$ hoặc $x-2=0$
$x=0$ hoặc $x=2$
7.
$x^2-3x=0$
$x(x-3)=0$
$x=0$ hoặc $x-3=0$
$x=0$ hoặc $x=3$
8.
$3x^2-4x=0$
$x(3x-4)=0$
$x=0$ hoặc $3x-4=0$
$x=0$ hoặc $x=\frac{4}{3}$
8 tháng 4 2021
a) f(x) = 0 ⇔ 4 - 5x = 0 ⇔ x = \(\dfrac{4}{5}\)
Nghiệm của f(x) là \(\dfrac{4}{5}\)
b)Không có nghiệm vì Với mọi x ∈ R thì \(x^2\) ≥ 0 ⇔ \(x^2\) + 4 ≥ 4 > 0
Do đó \(x^2\) + 4 > 0 hay \(x^2\) + 4 ≠ 0
Vậy f(x) không có nghiệm
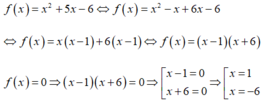
\(x^2-5x+4=0\)
\(\Leftrightarrow x^2-x-4x+4=0\)
\(\Leftrightarrow x^2-x-\left(4x-4\right)=0\)
\(\Leftrightarrow x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-4=0\\x-1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=4\\x=1\end{cases}}}\)
Vậy x = { 1; 4 }