Question

[Lê Hoàng Anh]

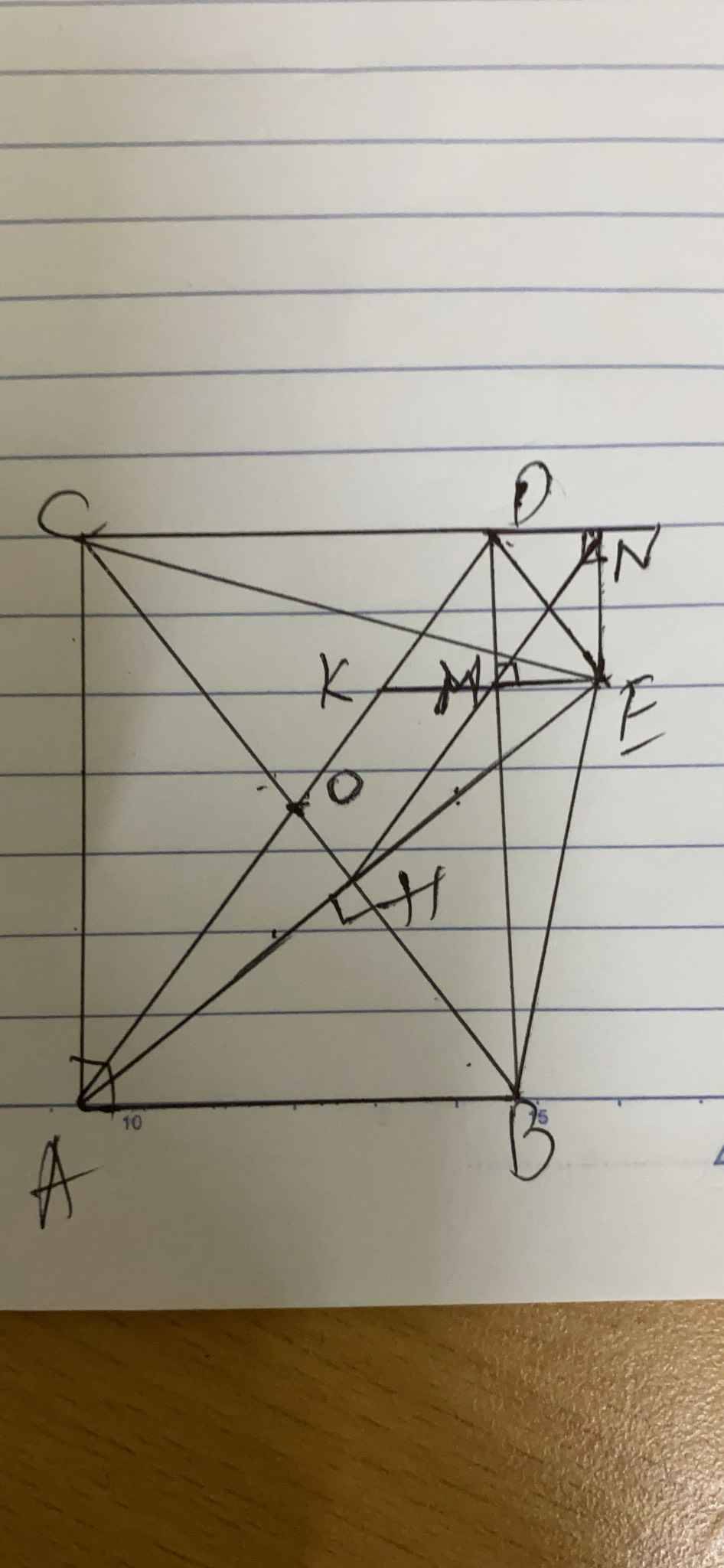
Bài 12:Cho tam giác ABC vuông tại A ( AB<AC). Đường cao AH. Gọi O là trung điểm của BC. D đối xứng với A qua O

a, Cm tứ giác ABDC là hình chữ nhật     

b, trên tia đối của tia HA lấy điểm E sao cho HE=HA.CM tam giác AED và tam giác BEC vuông           

c, Gọi M,N lần lượt là hình chiếu vuông góc của điểm E trên BD và CD, EM cắt AD tại K. CM DE=DK

d, CM: 3 điểm HMN thẳng hàng

Answer 1

[Nguyễn Duy Đạt]

a) xét tứ giác ABDC có AD cắt BC tại trung điểm O mỗi đường

→ ABDC là hbh

mà góc  A = 90^o ⇒ ABDC là hcn

b)xét △AED có OH là đường trung bình 

→ OH // DE 

AH \(\perp BC\) mà E nằm trên tia đối HA  

nên AE \(\perp OH\)⇒ AE \(\perp DE\)

⇒ △AED vuông tại E

**) xét △ vuông AHB = △ vuông EHB ( HB chung, AH = HE)

→ AB = EB(1)

xét △ vuông AHC = △ vuông EHC ( HC chung , AH = HE)

→AC = EC (2)

xét △ ABC = △ EBC 9(ccc) (từ 1 và 2)

⇒ \(\widehat{A}=\widehat{E}=90^0\)

⇒△ BEC vuông tại E

c)