Tìm cặp số nguyên x, y
a, x*y =x+y
b, x*y=x-y
c, x*(y+2)+y=1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\left(x,y\right)\in\left\{\left(-9;1\right);\left(-1;9\right);\left(-3;3\right)\right\}\)
b: \(\left(x,y\right)\in\left\{\left(1;7\right);\left(-7;-1\right)\right\}\)
c: \(\left(x,y\right)\in\left\{\left(11;-1\right);\left(-11;1\right)\right\}\)

a: \(\left(x,y\right)\in\left\{\left(-9;1\right);\left(-1;9\right);\left(-3;3\right)\right\}\)
b: \(\left(x,y\right)\in\left\{\left(1;7\right);\left(-7;-1\right)\right\}\)
c: \(\left(x,y\right)\in\left\{\left(11;-1\right);\left(-1;11\right)\right\}\)

a: M=x^2y^2(5a-1/2a+7a-1)
=(23/2a-1)*x^2y^2
M>=0
=>23/2a-1>=0
=>23/2a>=1
=>a>=2/23
b: M<=0
=>23/2a-1<=0
=>a<=2/23
c: a=2 thì M=22x^2y^2
M=84
=>x^2y^2=84/22=42/11
mà x,y nguyên
nên \(\left(x,y\right)\in\varnothing\)

M = 5x^2y^2+(-1/2ax^2y^2)+7ax^2+(-x^2y^2)
M=(5a+(-1/2a)+7a+(-1)) . x^2y^2
M= (23/2a - 1) x^2y^2
a)voi gia tri nao cua a thi M ko am
⇒M ≥ 0 ⇒(23/2a - 1).x^2y^2 ≥0
⇒23/2a - 1 ≥ 0 vi x^2y^2 ⇒0 ∀ x;y
⇒23/2a ≥ 0
⇒a ≥ . 2/23
⇒a ≥ 2/23
Vay a ≥ 2/23 thi M ko am voi moi x;y
b)Voi gia tri nao cua a thi M ko dg
⇒M ≤ 0 ⇒ (23/2a - 1).x^2y^2 ≤ 0 ∀ x.y
⇒23/2a ≤ 1
⇒ a ≤ 2/23
Voi moi a ≤2/23 thi M ko duong voi moi x;y
c) Thay a=2 vao M ta dc:
M= (23.2:2 -1).x^2y^2
M=22x^2y^2
De M=88 ⇒22x^2y^2 =88 ⇒x^2y^2=4
⇒(xy^2)= 2^2 ⇒ xy=2
⇒x= 2⇒y=1 ; x=1⇒y=2 ; x=-2 ⇒y=-1 ; x=-1y⇒-2
Vay(x;y)= ( (2;1); (1;2); (-2;-1); (-1;-2) thi M = 88
(ko danh dc dau cua chu ban thong cam cho mik)

a: xy=x-y
=>xy-x+y=0
=>xy-x+y-1=-1
=>x(y-1)+(y-1)=-1
=>(x+1)(y-1)=-1
=>\(\left(x+1\right)\left(y-1\right)=1\cdot\left(-1\right)=\left(-1\right)\cdot1\)
=>\(\left(x+1;y-1\right)\in\left\{\left(1;-1\right);\left(-1;1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;0\right);\left(-2;2\right)\right\}\)
b: x(y+2)+y=1
=>\(x\left(y+2\right)+y+2=3\)
=>\(\left(x+1\right)\left(y+2\right)=3\)
=>\(\left(x+1\right)\cdot\left(y+2\right)=1\cdot3=3\cdot1=\left(-1\right)\left(-3\right)=\left(-3\right)\left(-1\right)\)
=>\(\left(x+1;y+2\right)\in\left\{\left(1;3\right);\left(3;1\right);\left(-1;-3\right);\left(-3;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;1\right);\left(2;-1\right);\left(-2;-5\right);\left(-4;-3\right)\right\}\)

Đáp án D
Xét phương trình hoành độ giao điểm
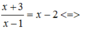
x2 – 4x – 1 = 0
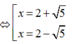
Giả sử A(2 + 5 ; 5 ); B(2 - 5 ; - 5 ) => yA + yB = 0

Bài 1:
a: \(\Leftrightarrow x-1\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{2;0;4;-2\right\}\)

Lời giải:
a. Thay $x=y$ vào điều kiện ban đầu thì:
$x+x=10$
$2x=10$
$x=5$
$\Rightarrow y=x=5$
Vậy $(x,y)=(5,5)$
b. Thay $x=y$ vào điều kiện đầu:
$2x+3x=180$
$5x=180$
$x=36$
$y=x=36$
Vậy $(x,y)=(36,36)$
c. Thay $y=2x$ vào điều kiện đầu thì:
$3x+5.2x=13$
$13x=13$
$x=1$
$y=2x=2$
Vậy $(x,y)=(1,2)$
a) Ta có: x=y
mà x+y=10
nên \(x=y=\dfrac{10}{2}=5\)
b) Ta có: \(\left\{{}\begin{matrix}2x+3y=180\\x=y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2y+3y=180\\x=y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y=180\\x=y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=36\\x=36\end{matrix}\right.\)
c) Ta có: \(\left\{{}\begin{matrix}3x+5y=13\\y=2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+10x=13\\y=2x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}13x=13\\y=2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
a,x=y=2