Bài 1 : Cho tam giác ABC vuông tại A. Gọi D là trung điểm cạch BC, E là điểm đối xứng với A qua D.a) Chứng minh : Tứ giác ABEC là hình chữ nhật.b) Trên tia đối của AB lấy F sao cho AF = AB. Chứng minh : AE song song CF.c) Tứ giác BECF là hình gì ? Cho BC = 10cm, AC = 8cm. So sánh diện tích hình chữ nhật ABEC và diện tích tam giác ACF. Bài 2 : Cho tam giác ABC nhọn (AB < AC) đường cao AK. Gọi D, E, F theo thứ tự là trung điểm của AB,...
Đọc tiếp
Bài 1 : Cho tam giác ABC vuông tại A. Gọi D là trung điểm cạch BC, E là điểm đối xứng với A qua D.
a) Chứng minh : Tứ giác ABEC là hình chữ nhật.
b) Trên tia đối của AB lấy F sao cho AF = AB. Chứng minh : AE song song CF.
c) Tứ giác BECF là hình gì ? Cho BC = 10cm, AC = 8cm. So sánh diện tích hình chữ nhật ABEC và diện tích tam giác ACF.
Bài 2 : Cho tam giác ABC nhọn (AB < AC) đường cao AK. Gọi D, E, F theo thứ tự là trung điểm của AB, AC, BC.
a) Tứ giác BDEF là hình gì ?
b) Chứng minh : Tứ giác DEFK là hình thang cân.
c) Gọi H là trực tâm của tam giác ABC. Gọi M, N, P theo thứ tự là trung điểm của HA, HB, HC. Chứng minh MF, NE, PD bằng nhau và cắt nhau tại trung điểm mỗi đoạn.
Vẽ hình cụ thể nhé. Cảm ơn nhiều.

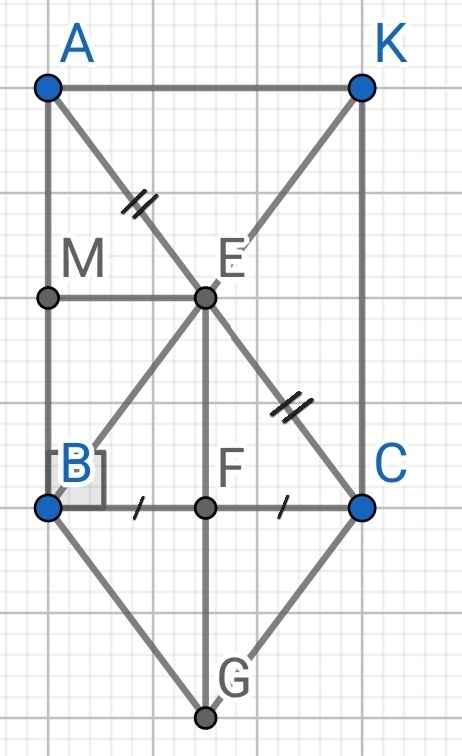
a) Xét △ABC có:
DA = DB (gt)
FB = FC (gt)
=> DF là đường trung bình của △ABC
=> DF // AC
Xét tứ giác ADFC có:
DF // AC (cmt)
=> Tứ giác ADFC là hình thang
b) Ở câu này đề bài cho bị thiếu △ABC cân tại B, vì nếu không có yếu tối này thì AF không thể bằng BG được. c) Xét tứ giác ABFH có:
AB // FH
AH // BF
=> Tứ giác ABFH là hình bình hành
=> AH = BF mà BF = FC
=> AH = FC
Xét tứ giác AHCF có:
AH // CF
AH = CF
=> AHCF là hình bình hành
=> AF // CH
d) Gọi M là giao điểm của AI và DH
Xét tứ giác ADIH có:
AD // IH
AH // DI
=> Tứ giác ADIH là hình bình hành
=> M là trung điểm của AI hay IM = \(\dfrac{1}{2}AI\)
mà AI = IC ( vì AHCF là hình bình hành)
=> IM = \(\dfrac{1}{2}IC\) =>IM=\(\dfrac{1}{3}MC\)
Xét △CHM có:
HK = \(\dfrac{1}{3}HC\)
IM=\(\dfrac{1}{3}MC\)
=> IK // MH ( định lý đảo Ta-lét)
hay IK // DH (1)
Xét △ABC có:
AF, CD là trung tuyến
mà AF cắt CD tại J => J là trọng tâm của △ABC
=> DJ = \(\dfrac{1}{3}DC\)
Xét △DHC có:
HK = \(\dfrac{1}{3}HC\)
DJ = \(\dfrac{1}{3}DC\)
=> JK // DH (2)
Từ (1) và (2) theo tiên đề Ơ-lít ta có: J, I, K thẳng hàng.