Question

[Trần Thị Thu Hiền]

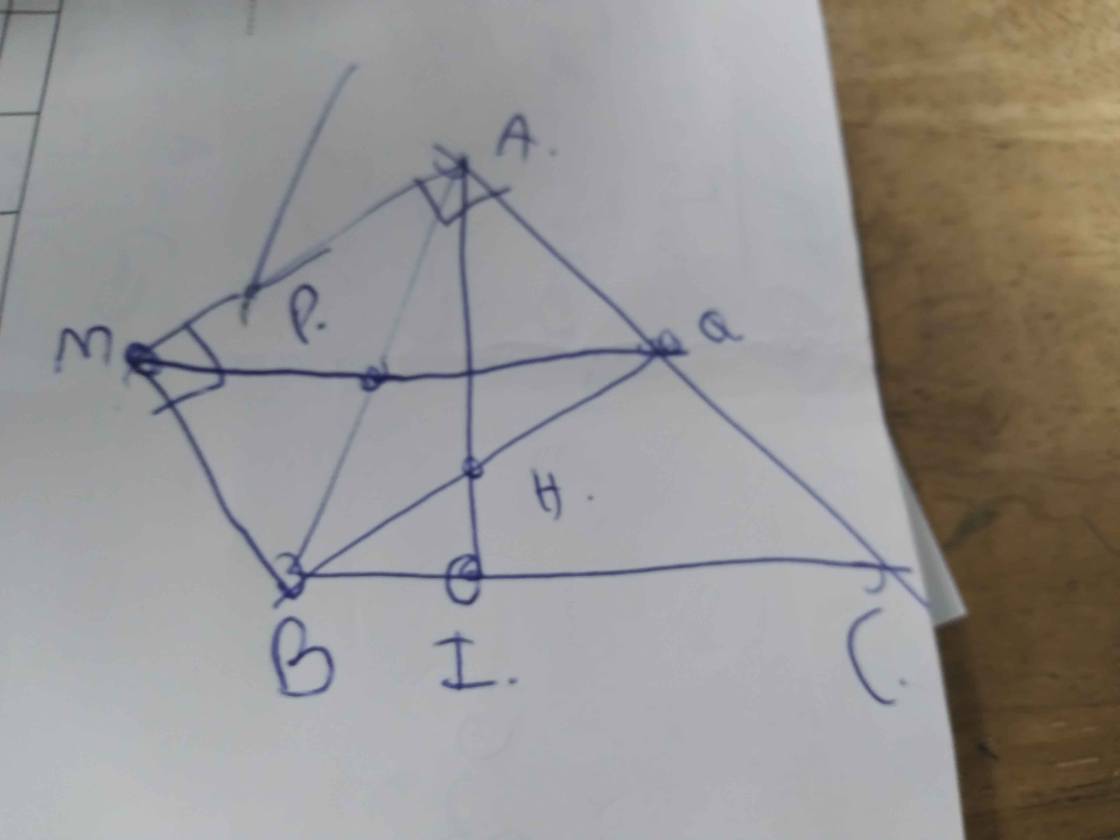
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm của AB, đường MP cắt AC tại Q và BQ cắt AI tại H

a) Tứ giác AMBQ là hình gì?

b) Chứng minh rằng CH vuông góc AB

c) Chứng minh tam giác PIQ cân

Answer 1

[Nguyễn Duy Đạt]

a) tứ giác AMPQ là hcn

b) ta có Ax \(\perp\) AC (gt)

M là giao điểm Ax và By ⇒ M ϵ Ax và M ϵ By

⇒ AM \(\perp\) AC

có BM // AC ⇒ AM\(\perp BM\)

xét △ APQ = △ BPM (gcg) ⇒ AQ = MB 

xét tứ giác AQBM có AQ //MB; AQ = MB; AM\(\perp BM\)

⇒ AQBM là hcn 

⇒ BQ \(\perp\)AC 

xét △ ABC có AI, BQ là đường cao cắt nhau tại H ⇒ H là trực tâm của △ABC ⇒ CH \(\perp AB\)

c) xét △ vuông AIB có P là trung điểm AB ⇒ IP =AP = PB 

mà AP = PB = PQ = MP( tc đường chéo của hcn)

⇒  IP = PQ ⇒ △ IPQ cân tại P