Giai phương trình nghiệm nguyên
x6 + 3x3 + 1 = y4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C.
⇒ Chia 2 vế phương trình cho x 3 ta được:
x 3 + 1 x 3 + 3 x 2 + 1 x 2 + 6 x + 1 x = m (*)
Đặt t = x + 1 x ⇒ t ≥ 2 , phương trình (*) m = t 3 + 3 t 2 + t - 6
Xét f ( t ) = t 3 + 3 t 2 + 3 t - 6 trên ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
f ' ( t ) = 0 ⇔ t = - 1
Bảng biến thiên:
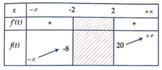
⇒ f ( t ) ∈ ( - ∞ ; - 8 ] ∪ [ 20 ; + ∞ ) ∀ t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
⇒ Phương trình f (t) vô nghiệm ⇔ m ∈ - 8 ; 20
⇒ Có 27 giá trị m nguyên thỏa mãn.

\(x^4+y^4=3y^2+1\Leftrightarrow-y^4+3y^2+1=x^4\ge0\)
\(\Rightarrow-y^4+3y^2+1\ge0\Rightarrow\frac{3-\sqrt{13}}{2}\le y^2\le\frac{3+\sqrt{13}}{2}\)
Mà \(y\in Z\Rightarrow y^2\)là số chính phương \(\Rightarrow y^2=0;1\)
*\(y^2=0\Rightarrow x^4=1\Rightarrow x=-1;1\)
*\(y^2=1\Rightarrow x^4+1=3+1\Rightarrow x^4=3\Rightarrow x\notin Z\)
Vậy phương trình có nghiệm nguyên \(\left(-1;0\right),\left(1;0\right)\)

Chọn đáp án D.
Bất phương trình tương đương với
![]()
![]()
![]()
![]()
![]()
trong đó hàm số f t = t 3 + 3 t đồng biến trên R
Vậy y c b t ⇔ x 2 - m x + 1 ≥ 0 , ∀ x
![]()
Có 5 số nguyên thoả mãn

Đặt f(x) = x4 - 3x3 + x – 1.
f(x) là hàm đa thức nên liên tục trên R.
Ta có: f(0) = -1 < 0
f(-1) = 1 – 3.(-1) – 1 – 1 = 2 > 0
⇒ f(0).f(-1) < 0
⇒ f(x) = 0 có ít nhất một nghiệm xo ∈ (-1; 0) ⊂ (-1 ; 3).
Do đó phương trình đã cho có nghiệm xo ∈ (-1; 3).
→Xét x ≥ 1 thì:
x⁶ + 3x³ + 1 > x⁶ + 2x³ + 1 = (x³ + 1)²
và x⁶ + 3x³ + 1 < x⁶ + 4x³ + 4 = (x³ + 2)²
=> (x³ + 1)² < y⁴ = x⁶ + 3x³ + 1 < (x³ + 2)²
=> y⁴ nằm giữa 2 số chính phương liên tiếp
=> pt đã cho vô nghiệm với x ≥ 1
→Xét x = 0: tính được y = ± 1 => pt có 2 nº (0; -1) và (0;1)
→Xét x = -1: y⁴ = -1 (vô nº)
→Xét x ≤ -2: để dễ nhìn đặt z = -x => z ≥ 2
pt trở thành: y⁴ = z⁶ - 3z³ + 1
Ta thấy: z⁶ - 3z³ + 1 < z⁶ - 2z³ + 1 (vì z ≥ 2)
=> z⁶ - 3z³ + 1 < (z³ - 1)²
và (z⁶ - 3z³ + 1) - (z⁶ - 4z³ + 4) = z³ - 3 > 0 (do z³ ≥ 8)
=> z⁶ - 3z³ + 1 > z⁶ - 4z³ + 4 = (z³ - 2)²
Do đó: (z³ - 2)² < y⁴ = z⁶ - 3z³ + 1 < (z³ - 1)²
=> y⁴ nằm giữa 2 số chính phương liên tiếp
=> pt đã cho vô nº với x ≤ -2
Kết luận pt đã cho có 2 nº là (0; -1) và (0;1)
→Xét x ≥ 1 thì: x⁶ + 3x³ + 1 > x⁶ + 2x³ + 1 = (x³ + 1)² và x⁶ + 3x³ + 1 < x⁶ + 4x³ + 4 = (x³ + 2)² => (x³ + 1)² < y⁴ = x⁶ + 3x³ + 1 < (x³ + 2)² => y⁴ nằm giữa 2 số chính phương liên tiếp => pt đã cho vô nghiệm với x ≥ 1 →Xét x = 0: tính được y = ± 1 => pt có 2 nº (0; -1) và (0;1) →Xét x = -1: y⁴ = -1 (vô nº) →Xét x ≤ -2: để dễ nhìn đặt z = -x => z ≥ 2 pt trở thành: y⁴ = z⁶ - 3z³ + 1 Ta thấy: z⁶ - 3z³ + 1 < z⁶ - 2z³ + 1 (vì z ≥ 2) => z⁶ - 3z³ + 1 < (z³ - 1)² và (z⁶ - 3z³ + 1) - (z⁶ - 4z³ + 4) = z³ - 3 > 0 (do z³ ≥ 8) => z⁶ - 3z³ + 1 > z⁶ - 4z³ + 4 = (z³ - 2)² Do đó: (z³ - 2)² < y⁴ = z⁶ - 3z³ + 1 < (z³ - 1)² => y⁴ nằm giữa 2 số chính phương liên tiếp => pt đã cho vô nº với x ≤ -2 Kết luận pt đã cho có 2 nº là (0; -1) và (0;1)